*
APPLICATIONS
Let us now give some attention to the application and significance of the formal system we have established, based on three operators: a fourfold, a threefold, and a twofold.
The fourfold operator
The fourfold operator applies to analysis, concepts, forms. Consisting of two dichotomies that are mutually orthogonal, or independent, it tells us that in any situation that can be dichotomized, or divided into two opposite aspects, there must exist a second dichotomy which mediates or measures the first.
Consider the old story of Solomon and the two women. Both claimed possession of the baby, so Solomon proposed that the baby be cut in two and each woman given half. One woman agreed. The other said no: she would rather give up possession of the baby and have it live. Solomon recognized the latter as the true mother and gave her the baby.
What happened? Solomon split the dichotomy of possession by introducing an independent dichotomy: the being of the baby as opposed to its nonbeing. Under this scrutiny, like that of a painting under x-ray, the false mother was revealed.
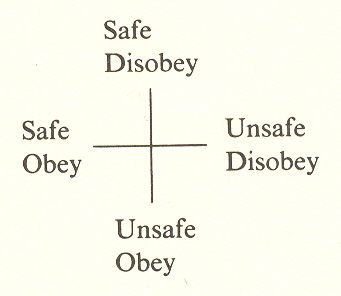
Problem: A married couple quarrels. The wife wants to go into a field, the husband insists that she must not because there is a dangerous bull in the field. The wife says the bull is not dangerous.
If we recognize that the situation contains two issues, safety and obedience, we can combine them differently: We ask the wife if she would obey her husband if the bull were really dangerous. She says no. We ask the husband if he would insist on the wife's obedience even if the bull were not dangerous. He says yes. Obviously, the couple is arguing about obedience, not about the bull.
Generally speaking, we try to discover two independent issues between the two parties. We describe the claims of the two parties in two opposite word pairs.
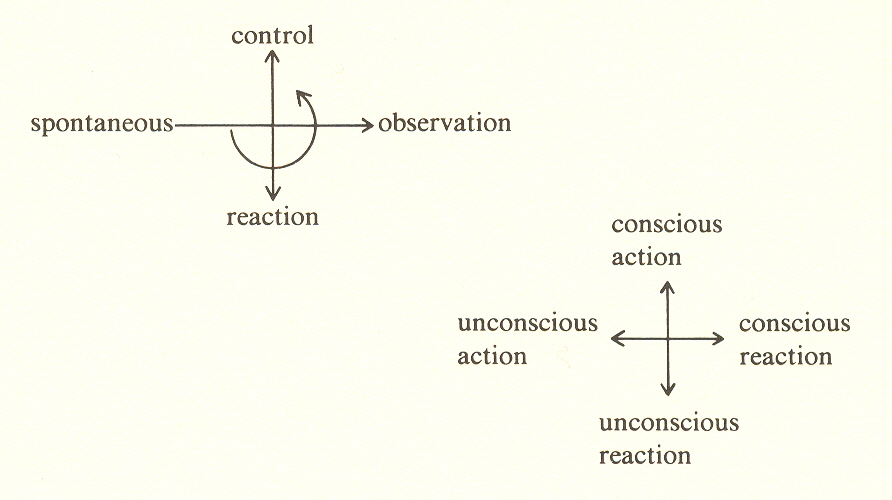
Once this is done, the rest is easy. We take the two word pairs and cross-product them. Recall the learning cycle in which the infant reaches out and touches things (an example which dealt with kinds of action). In that case, we were able to describe step 1 as unconscious action and step 3 as conscious reaction (both words opposite). The other pair then become (2) unconscious reaction and (4) conscious action.
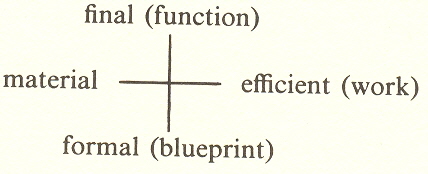
The same principle can be applied to kinds of relation, or kinds of "things." Take, for example, the contributing factors in a clock (relating them to Aristotle's causes):
Factors Aristotle
A clock's function, to keep time Final cause
The material of which it is made, brass Material cause
The plan to which the parts conform, the Formal cause
blueprint
The work of putting it together Efficient cause
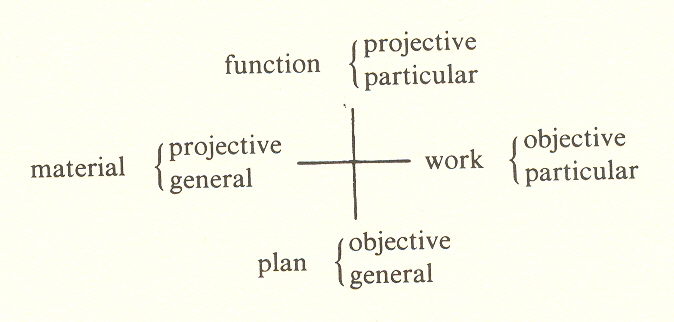
Now let us fit these causes' into "pairs of opposites":
Obviously, the function is projective. The blueprints are objective. Since the work of assembly is also objective, we are forced to say the material is projective. This may seem untrue until one realizes that the brass could be used for many things besides the clock. This indicates also that the material is general; hence, the work is particular.
We have to choose whether the plan is particular or general. It has to be general because any number of clocks can be made from it. This leaves us with timekeeping, the function, as particular. Here we must recognize that timekeeping, while it seems a general function, actually is not. That is why one can ask "What time is it?" and expect a particular answer. If the watch kept general time, it would not mean anything at all.
The very difficulty of this example tells us what to look for in others. We must overcome the scientific habit of confining attention to what is true generally and objectively, while omitting what is true in the particular situation. Of course, an observed fact is always particular, and it is often very important to give attention to such facts. But this warning has often been stated. What is difficult is the projective particular, the existence in every situation of a "pointingness" that is not general. Like the question "What time is it?" it has one and only one answer, and this answer varies from moment to
Obviously, the function is projective. The blueprints are objective. Since the work of assembly is also objective, we are forced to say the material is projective. This may seem untrue until one realizes that the brass could be used for many things besides the clock. This indicates also that the material is general; hence, the work is particular.
We have to choose whether the plan is particular or general. It has to be general because any number of clocks can be made from it. This leaves us with timekeeping, the function, as particular. Here we must recognize that timekeeping, while it seems a general function, actually is not. That is why one can ask "What time is it?" and expect a particular answer. If the watch kept general time, it would not mean anything at all.
The very difficulty of this example tells us what to look for in others. We must overcome the scientific habit of confining attention to what is true generally and objectively, while omitting what is true in the particular situation. Of course, an observed fact is always particular, and it is often very important to give attention to such facts. But this warning has often been stated. What is difficult is the projective particular, the existence in every situation of a "pointingness" that is not general. Like the question "What time is it?" it has one and only one answer, and this answer varies from moment to moment.
We have already used the map example, but it would pay to note once more the great difference between the kinds of information that fall under each of the map's four aspects. The one we are most accustomed to, because it is intellectual, is the map as a statement of relationship between geographical points. From the map we can see that Albany is between Buffalo and Boston, and so on. We cannot know how long it will take to get from one place to another unless we have additional information, the scale (under which we include the mode of travel, whether we walk, ride, fly, etc.). This information is not on the map. It involves reality. We need to draw on experience. Distances in New York State and distances in the Himalaya Mountains might have the same appearance on a map, but involve altogether different orders of difficulty in their actual traverse.
Here we must not be misled by the fact that scale can be stated as a ratio on the map, because the ratio does not supply the missing ingredient, which must come from experience. On the map it says "10 miles to the inch," but we must know what a mile is. We cannot get this from a map. We might have walked a mile to school when we were young, or run a mile in five minutes on the track team, but our experience of a mile did not come from the study of geography books. It is of a different nature than the conceptual grasp of relationship.
Next, "Where are we on the map?" This is particular and objective: particular because it is a present fact, and objective because it can be communicated to others. This gives no difficulty because, since it is objective, it is given recognition by science, though logic might not accept it because logic gives no formal recognition to facts as such.
Finally, we come to the particular projective. "Which way to Detroit?" (We need know only one orientation. This, together with the map, will provide any other orientation.) But this is particular and projective: particular because it changes as we move about, and projective because it literally projects. It doesn't tell us a present fact, but a future fact. Hence, it is projective.
Note that we are talking in every case about the whole situation. The map is dealing with information about the terrain, to be sure, and may include a great deal of information about the location of towns, roads, etc., and a scale of distances. The significance of the fourfold information is that it goes further: it also includes, or has room for, your participation in the situation, how much effort and time will be required of you, and by its inclusion of the compass, makes it possible to include an ultimate goal, which objective science has to ignore.
The threefold operator
The threefold operation is an entirely different way of cutting the cake. It is much more fundamental, and it cannot be analyzed.
For this reason, it is difficult to write or talk about, although from the point of view of philosophy or of life, the threefold is fundamental.
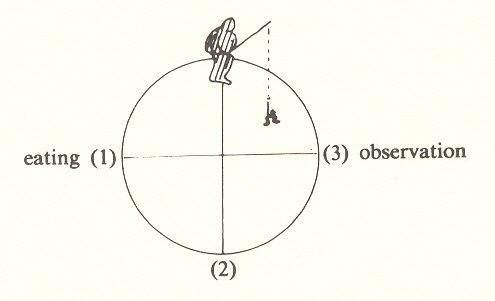
In fact, the threefold is the natural way we move in life. We see something, buy it, and enjoy it: food, eating, satisfaction; stimulus, response, result. There are three categories of terms: relations, acts, and states. The reader will recall the difficulty of finding sufficiently general words.
To implement description, it is helpful to correlate the three categories to past, present, and future. The relation category correlates to the past because it is generally that which already is. The action category is in the present because all action is in the present. You are now reading this book. The state or affective category applies in general to the future in the sense that it is the result of action.
But it is also possible for the state to come first. I'm hungry, so I look for food. The state leads to the action.
Perhaps what makes the threefold so elusive is that whatever is named becomes a "relation" term: "Would you like to play tennis?" The action here is not playing tennis, but the question "would you like." "To play tennis" is held up as an object. This takes us into the complexities of grammar, for we must distinguish the principal verb from the infinitive phrase.
In fact, despite the risk of added complications, it is of interest to compare the basic structure of the sentence with the threefold, for the sentence has three principal parts: subject, verb, and object. "The hunter shoots the bird." The similarity is greatest in that the verb contains the action which produces a result. To press the similarity further creates problems, for in the sentence, A acts on B, one thing acts on another, whereas the threefold would make the action of the hunter transform the bird into a museum specimen. The threefold seems to deal in a wider range of significance. We are interested in what the hunter proposes to do with the bird - what is the result? Without this information, the threefold is incomplete.
Another characteristic of the threefold is that it is so natural that it blends into life; it does not "stand out." Indeed, we might suspect that there is a tendency, in the matter of philosophic norms, for the empty wagon to make the most noise. Dr. Johnson kicked the stone to prove that it existed, that it was objective, but both the word "object" and the word "exist" denote something that stands out or against. Against what? Since the word "object" derives from the Latin ob, "against," and jacere, "to throw," there must be something for the object to oppose, and this "throw" or projection is as much a part of reality as is the object. The threefold is this ongoing movement from one state to another, which takes place in time, or we can even say is time. In any case, it is experience and contains situations, actions, and results.
The fact that only the relation part of this can be communicated and defined leads to the quite erroneous insistence by philosophers on objectivity as a criterion of reality. Scientists, however, whatever they may say about objectivity, use all twelve measure formulae. But the measure formulae cannot all be objective. If we use tangibility as a criterion of reality, acceleration, which is immediately felt, is real, velocity is not. If we use visibility as a criterion, position is visible, velocity and acceleration are not, and so on.
Psychologists and teachers are discovering likewise that animals or children cannot learn without doing. They find that the learning process does not consist of filling a creature with information, as one would program a computer, but of active interaction with the environment.
But in these instances, the scientists are still seeing only from the outside. As manipulators, they are not experiencing the terms they manipulate. To talk about the force of attraction is quite different from to be hungry or to be in love. The scientist speaks of gravitational force and nuclear force with the same aplomb despite the fact that the latter is
times greater. Why not? Well, just to display this difference on the same graph would require that we compare the diameter of the universe (
centimeters) to its smallest possible distance, the diameter of a proton (
centimeter).
It is customary to think of love, attraction, pleasure, pain, etc., as subjective, not "out there" in the universe. Hume is immortalized in histories of philosophy because he showed that we do not know causality objectively. It is a mental habit. The history of Western thought has tended first to divide the universe into interior and exterior, and then to discredit the interior by saying it is not there, or is purely "subjective," by which is meant interior to persons.
What is overlooked in this reasoning is that the universe also includes the nonobjective factor. The proton attracts the electron; the nuclear force binds the atom; the planets move in closed orbits; the universe has feelings. Physicists call them forces. To deny their existence in favor of objective "formulations" is pure sophistry.
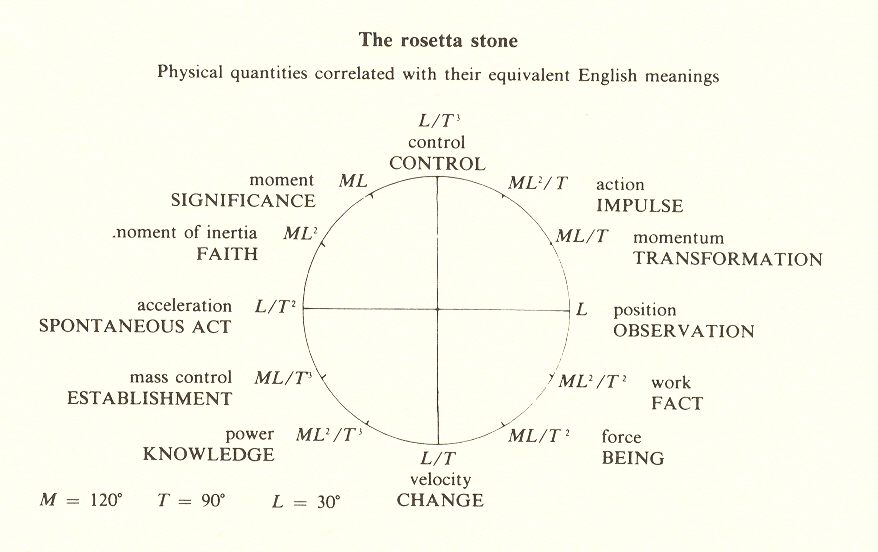
In sum, we have shown that the threefold, despite the seamless quality which makes it difficult to get "hold of," is still implicit in the measure formulae of science. These expressions, which constitute a basic vocabulary of science, fall into three groups of four.*
*The last column is displaced one place from the tabulation in Chapter IV in order to have the three members on each line 120 degrees apart.
We need not review here the English meanings we are able to attach (see "Rosetta Stone" diagram). The point we wish to emphasize is that the measure formulae bear witness to the important status of the threefold in science.
There remains an important point that has not been covered. We have mentioned that the threefold can be correlated with past, present, and future. But we could go further, for the threefold may be even more basic than time, in the sense that it gives to time not only its customary division (past, present, and future), but its directionality.
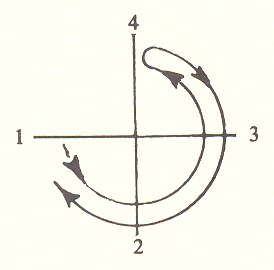
The direction of time, like other aspects of the threefold, is not objective, and it cannot be communicated as we communicate comparative measures (by drawings, definitions, etc.). Immersed in time's flow, we have no opportunity to get outside it. And the threefold involves this directionality. If represented by three letters a, b, c, we can have two possibilities, abc and acb. Analytically, we can say that a is between band c, but we have no way to say that a is before b except by reference to "subjective" time.
The choice of which way to go, abc or acb (clockwise or counterclockwise), takes us to the twofold operator.
The twofold operator
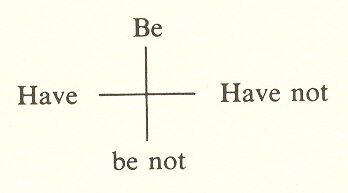
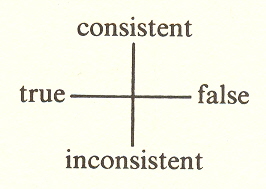
This is the most difficult operator. It is the one that gives the threefold its direction. We can have only two such directions, and this is why the twofold is different from one of the dichotomies in the fourfold. We might have thought, for example, that true and false is a dichotomy, but the teaching here is that it is not. It is one of two pairs of opposites that belong together in a fourfold. Thus we would have:
And note that this is just how it occurs in fact. We don't ever have a situation in which true and false suffice to describe it.
Take, for instance, a lawyer cross-examining a witness. He says, "Where were you on the night of. . . ," etc., and continues in this way until the witness makes some inconsistent statement. The lawyer can recognize the inconsistency and use it to smoke out the true, much as Solomon uncovered the true and false mothers.