*
THE TURN
Out of the nettle, danger [determinism]
Pluck the flower safety [freedom]
Apologies to Hotspur, in Henry IV
Requirements for the turn
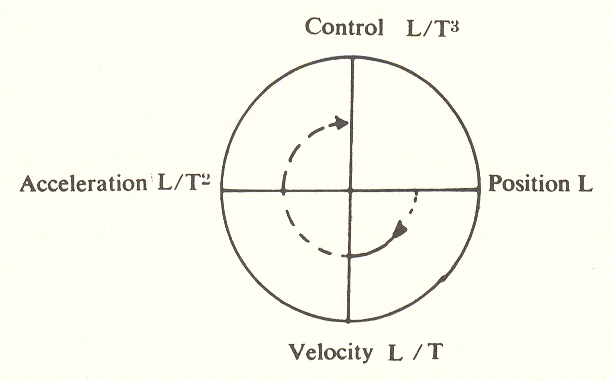
The discovery of a third derivative is important, for it shows how we may draw on the foundation of Newtonian mechanics for a very different conclusion from the determinism it was thought to imply. The third derivative, which we have called control, describes the control of acceleration (or of force, if we add mass to acceleration). This is action, a rebirth of the first cause at level I.*
*First cause with the photon at level I is action
In this physical world, first cause is the implementation of self-control.
Their product is
1, hence
which is action, not to be confused with the simpler control of force, or
To put this in English: the physical world is the state of affairs in which the parts have been separated out; it is populated with objects, forces, distance, time. But when we know how to control force (when we multiply
we create the "turn."
But our task is not over; in fact, we have done little more than to advance our physics up to the sophistication of our instinctive inheritance, for we continually have access to control, not only in driving automobiles but in all kinds of motion: walking, talking, or even just standing upright. What we must now show is not only that it is possible to control machines, but that it is possible for a living organism to control itself.
We must discover, now that we have control as an option, just what is required in order that control be possible. Given a machine that can be controlled, and given a hypothetical monad* - a ghost, if you like how can the ghost control the machine?
*This is my first use of the term "monad." Up to this point it was the quantum of action, but now it acquires status as the vital spark in life.
Here is where the arc makes intelligent handling of the question possible, for the arc shows that it is at level IV that life begins and that it is at that point we should look for the control situation.
This is the realm of molecules and so, on the basis of the arc, we can assume that there is a point in molecular evolution when a molecule starts to build up energy and begins to move against entropy. The polymers are an example of just this phenomenon. They build themselves, and the process, unlike a crystal, can be endothermic: it can store energy and cool the environment.
Polymers (chain molecules) are not life in the usual sense, even though they grow and replicate themselves; but they show that a molecular phenomenon that reverses entropy can occur.
The beginning of life
This is the crucial step, for it implies that the monad, after its long precipitous descent from an energy level of a billion electron volts to the fraction of an electron volt involved in these molecular bonds, has at last taken the wheel and begun to climb out of the abyss.
I am not particularly disturbed by invoking a sort of molecular intelligence here. We must understand that our cosmology should provide the necessary equipment for this crucial step, even if it doesn't provide or explain the act of will which brings it about. This bottom of the arc is the prodigal son situation. The return does not come about because of the law; it must be voluntary, and has to wait until this point because not until now is there a basis on which to build a return.
Molecular bonds and temperature
We have already mentioned molecular bonds at level IV (Chapter IV). These bonds are, as it were, the "last stand" of the quantum of action which here, at the molecular level, acts to hold the parts of a molecule together. We may think of this bond as an energy, because it requires energy to pull apart that which the bond holds together. Such molecular bonds, once formed, do not of themselves come apart. However, they may be separated if the molecule is struck hard enough by another molecule. How hard must it be struck? Enough so that the energy of impact is equal to the energy of the bond.
It is at this point that the temperature of the environment comes into play. The environment consists of other molecules batting themselves about in a random fashion, and the temperature of this environment is the rapidity of this motion, which imparts to each molecule an average kinetic energy which is greater as the temperature is greater. When the temperature is high enough so that the energy of the average molecule approaches that of the bond, the molecules begin to split up. It is this fact that is made use of when metallic ores such as iron oxide are heated in a furnace to drive off the oxygen and release the pure iron. Or again, where crude petroleum is heated and the heavy-oil molecules are broken down into smaller gasoline molecules. Many chemical operations make use of this principle that chemical bonds are broken by the use of heat. The cooking of food is a familiar example.
Now we know that life is peculiarly sensitive to heat. Cooled to the temperature of a household refrigerator, most life forms cease their processes - including the activity of decay bacteria; the food is preserved. Heated to a temperature somewhat over 100º Fahrenheit, most life ceases. Milk is pasteurized at 140º, which kills the disease bacteria. This temperature range for active life - from approximately 23º to 221º Fahrenheit - is a relatively narrow one. For warm-blooded animals the range (excluding hibernation) is still smaller, from 94º to 113º Fahrenheit, a tiny span if one considers the range between absolute zero (-459.4º F) and the temperature at the surface of the sun (10,800º F).
Life can exist only within this narrow range. Why? The answer must be that the chemical bonds on which life depends cannot be formed at temperatures below the lower limit and cannot be maintained above the upper limit. Life requires this temperature to make the energy transactions that maintain it.
We also know that the most basic characteristic of life is that it can reverse entropy, that is, it can store order in contrast to the tendency of nonliving matter to reduce order (or increase entropy; i.e., stones tend to roll downhill, not uphill). Thus vegetation takes energy from sunlight to store it in starch and sugar, and animals consume vegetation or other organic material to rebuild it into their own bodies. Neither one creates the energy they store; they extract it from their environment.
This is what life does. We can see that it occurs, and we can even analyze the steps by which it occurs, much as we can follow the steps by which a carpenter erects a building out of the material he obtains at the lumber yard. But this does not explain the whole process either as life does it or as the carpenter does it. To explain the carpenter, we can speak of "purposive action," but the dictates of 19th-century mechanistic science (determinism) forbid our speaking of such purposive action at the molecular level. (Indeed, they forbid our speaking of it at any level. But at the human level - that of the carpenter - we have the direct testimony of experience which overrides the theoretical assumptions of determinism.)
Quantum mechanics brings forward new evidence to show that the prohibition of mechanistic science is invalid for individual particles. Electrons and atoms bounce about in unpredictable and random fashion; their behavior cannot be distinguished from that of free entities.
How does this new ruling apply to molecules? Here is where the temperature factor is important. For there is a temperature range in which the molecular bond behaves in a free or random fashion. It can break apart or not break apart, depending on whether it is in phase or out of phase with the incident energy that is bombarding it. This point is self-evident, but the interpretation which makes it the entry point of free will (see above) is my own.
The molecule is in this respect like a wrestler who can react either with or against his opponent and by correct timing defeat a heavier man.*
*This is the kind of action in which Maxwell's demon engaged. But note that the demon, like a wrestler, interacts directly; he is not required to observe and compute as is his more intellectual counterpart - the Heisenberg observer - and thus does not require energy. This disposes of the current claims (based on energy requirements) that the demon has been exorcised.
The choice of timing is the only freedom left to the molecule at substage four, and it affords the opportunity for the monad to reverse its fall into determinism and, by collecting energy, to create the organization (substage five) which will begin the ascent back to freedom, this time with greater scope.
Timing is the ingredient that marks success in any field, whether it is the wrestler who overcomes a more powerful opponent, the success of a business venture, the performance of a musical composition. It is not energy; it is not force, nor even the control of force; it is the correctly timed control of force, and it has to be learned.
The fact that it has to be learned is important, for it explains the descent (the fall); it explains why process goes so far out of its way to achieve its ultimate goal, and it explains why the world is as it is.
The "turn," then, is the origin of life and it depends on timing, the hidden freedom of level IV. The turn is the most important point of the whole arc, and while we cannot completely explain it, it is essential that we make room for it in our theory.
We should now implement the above heuristic description with a more formal explanation. This is possible now thanks to Eddington's profound insights reconciling quantum theory and relativity. Since this involves concepts difficult even for the physicists, the general reader may prefer to move on to the next chapter (Atoms). I would urge him, however, to note the section entitled "Comparison with classical physics," which accents important points by comparing the present theory with the older view of a universe determined by laws but unable to account for life.
Explanation of the phase dimension
Perhaps the greatest contribution of the theory of relativity is that it adds a new dimension to the known physical universe. This dimension is not time, despite the impression we may have received from popular accounts of time as the fourth dimension. Rather, it is what Eddington calls phase.* Eddington goes on to show that, beginning with the ordinary physical universe represented as a sphere, when we include phase we widen the universe in another dimension perpendicular to space-time.
*This is not phase in the sense of Gibbs. It is rather phase in the sense of a lead or lag, as in the case of alternating current, in which voltage and current may be out of phase.
An additional factor of 3/4 must be introduced to stabilize the scale. To get the higher dimensional universe (the Einstein hypersphere; see Appendix II), we multiply the volume of the three-dimensional sphere by these two factors,
The phase dimension, an uncertainty of
, describes the maximum possible range of angle, 360°. It is a circle. And I would add it is also a cycle, the cycle of action, and stands in place of time. We might have expected the formula for the universe to express the time dimension as well as the three spatial dimensions, but instead it describes time in much the way that we do when we speak of a person's lifetime, not in years but in terms of birth, youth, maturity, middle age, etc.
This extra phase dimension is the observer's uncertainty as to which direction a thing will move. As Eddington points out in Fundamental Theory (see Appendix III), it applies to each particle or small system. Here in what is surely one of the most remarkable passages in scientific literature, he opens his Chapter III by dropping the curved space of molar relativity and replacing it by the uncertainty, that is, by the curvature of
Since
Important as this point is - and I'm afraid it is sadly neglected in high quarters - our task lies in going still further, in the recognition of the significance of this
It is our hypothesis that this range of angle, which to the observer is uncertainty, is a range of choice. We may think of this choice as either a choice of direction or a choice of timing.
But we should not neglect the other factor of 3/4. This factor is what Eddington calls "stabilization of scale." From our point of view, this stabilization of scale is "self-limitation" or control, the same control we referred to at the end of Chapter IV, which arises in the cycle of action at the point 3/4 of the way around the circle or cycle of action.
To assist in the understanding of this crucial point - that control is 3/4 of a circle - we can invoke what is known in psychology as the learning cycle. The learning cycle refers to the trial-and-error process by which a child learns to avoid a hot stove, a rat learns to tread a maze, or even a flatworm to avoid an electric light.
This cycle begins at (1), when random action (equivalent to acceleration) encounters some painful experience, say a hot stove; it then reacts by withdrawal at (2) ; and at (3) associates the pain with the stove (conscious reaction). After this sequence, it can, at (4), consciously* avoid the hot stove. This is control, but it is achieved by a different route from that of the derivatives: it moves counterclockwise from (1), whereas the derivatives proceeded clockwise from (3). The derivatives are the basis for sophisticated or informed action, whereas the learning cycle is the reverse of this, the process by which control is learned in the first place.
*If one objects to the word "consciously," we can say, with the behaviorist, that the pain is associated with the hot stove.
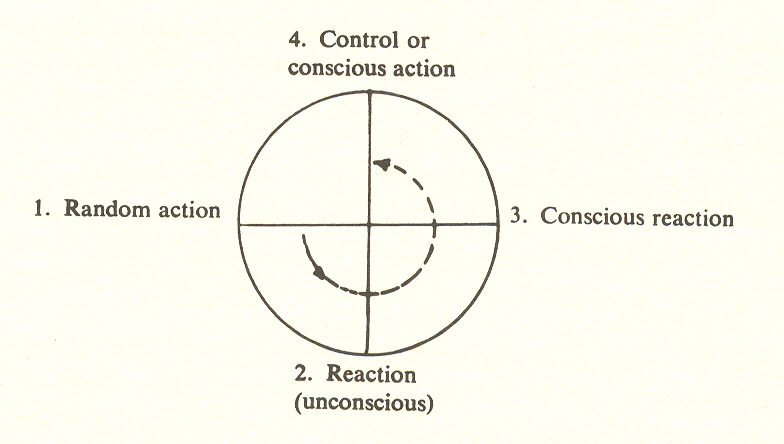
While this need not be consciousness as we know it - its duration is still but a trillionth of a second (ours, it would appear, is about 1/10 of a second or less) - yet it is the consciousness appropriate to a molecular bond, meaning that by control of phase or timing, it can lock or unlock such bonds.
This range of choice is indeterminate from the point of view of the observer and, by the same token, is freedom for the "entity," i.e., the bond. In other words, the quantum of action is now able either to absorb or to release energy and hence is able to break the inevitability of the second law of thermodynamics (increase of entropy).
We must be careful, however, to distinguish this from the reversal of entropy, which can be achieved by purely mechanical devices. A self-winding wristwatch is an example. Here the random movements of the wearer's arm serve to induce rotation which winds a spring. The opposite rotation, which would unwind the spring, is prevented by a ratchet. Such a device could also operate on a molecular scale, and may serve as another adjunct to life, but it does not explain the act of will to which we referred a couple of times in Chapter IV. To account for the essential freedom of will, and the option of life to store and release energy, we require the free phase dimension. The free phase dimension, then, is that which makes it possible for the quantum of action to control timing.
Comparison with classical physics
Let us now consider the quite different view of the universe which the theory of process invokes, as compared with that of classical physics.
Classical physics Theory of process
The universe is based on law. The universe is based on freedom.
Laws, constraints on freedom,
are secondary.
It deals with molar objects It deals with individuals (quanta
(statistical aggregates). of action, single atoms,
molecules, and organisms).*
Objects are fundamental. Action is fundamental.
*The theory of process recognizes that an organism can be under the control of the quantum of action, as can a molecule. If this were not so, how could an organism grow from a single cell?
In the theory of process, laws remain important, but they do not have the omnipotence which classical physics assumes. Process, in fact, emphasizes the importance of non-law, or uncertainty, because of its positive contribution, especially to the emergence of life in higher kingdoms. (It is in these higher kingdoms that the change in degrees of certainty described in Chapter IV makes its major contribution.)
Additional information
Different kinds of law at each level
A further aspect of the theory, which can usefully be mentioned in conclusion of this chapter, is that the several levels exhibit different kinds of law.
It is interesting to note that we may characterize the four levels by the different degrees to which they obey the law. This shows up in a simple mathematical manner, in the degree of the relevant equations, whether linear or quadratic.
Level I. Here, if we are careful to realize what is going on, we find that, except for hierarchy, there are almost no "laws." The speed of light, as we said earlier, is not a restriction on light, but rather a boundary condition on matter; not a boundary to space, but a boundary to the combination of time, i.e., velocity. Law of distribution breaks down:
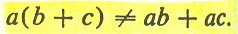
Equations here reduce to stating a constant. Action = h. Velocity of light = c.
Level II. The realm of linear algebra. Laws of conservation (mass, charge, spin, etc.).
Here there is one degree of constraint. The location of an event in time is an example. Laws here must in consequence be linear, laws of numerical summation.
