*
APPENDIX II
SEVEN-NESS
The intelligent reader is likely to regard with suspicion a theory which bases itself on the number seven.
Why? Is it because any reference to seven conjures up the prescientific? Legend, myth, fairy tales, and even superstitions are encumbered with sevens for no apparent reason and, by giving this number a mystique that the modern mind cannot accept, have given it a bad reputation.
As I stated in the Introduction, my first contact (since nursery days) with the occurrence of this number in ancient cosmologies affected me similarly: it rubbed me the wrong way. However, when I realized that topology, a science that deals with even more profound implications than does geometry, could supply formal reasons for a sevenfold ordering, I was prodded into a rethinking of the concepts embodied in relativity whose theories of curved space-time had provided the foundations for modern speculation on the nature of the universe.
My early curiosity about first principles, coupled with the publicity given, at the time, to the theory of relativity ("only twelve scientists could understand it" was what the press notices gave out), led me to request it as my major. Whether the pupil was ready I shall never know, but the master appeared. He was Oswald Veblen, perhaps the foremost American mathematician of the time, and he willingly took me on as his sole student for the two remaining years of my college career. Each week I would read and copy his manuscript of his version of the mysterious new subject. My other text was Eddington's Mathematical Theory of Relativity.* Both placed great emphasis on the "summation convention," which was a mathematical shorthand that permitted one to write countless equations with a few Greek squiggles. Even when I could sometimes get the hang of this painful exercise, I still wanted to know what it all meant, and would constantly harass Veblen for enlightenment. This, Veblen would tell me, was not the business of mathematics. I must learn to manipulate the language; the mathematician should not concern himself with meaning.
*Eddington, Sir Arthur Stanley. Mathematical Theory of Relativity. New York: Macmillan Co., 1923.
Nevertheless, something did seep through, and Veblen in his unguarded moments would occasionally grant me indulgence, enough to keep my curiosity alive.
After leaving Princeton, I continued to ponder on the questions raised by relativity and the adequacy of its answers, and to try to keep abreast of the more significant but less publicized findings of quantum theory; I kept in touch with Veblen, who meanwhile had moved to the Institute for Advanced Study, which he directed. But I could sense that his interest in mathematics was waning; he showed more concern for the lawn. And Bertrand Russell, who once through mutual friends chanced to come to my house in Paoli, and whom I cornered in order to explain my solution to the paradoxes he had bequeathed to posterity, hastened to assure me that he was no longer interested in mathematics, he had transferred his attentions to women. In any case, aside from my occasional visits to Veblen, which I renewed after the helicopter was completed, and courses in logic which Veblen insisted I take before he would introduce me to Goedel, my career has been ex cathedra (though I did my homework, Veblen died before he could introduce me to Goedel).
But to return to relativity. Einstein's contribution (or rather, as Veblen used to insist, that of the mathematicians before him, Riemann, Lobachevski, et al.) was to provide a more generalized geometry, a curved space-time, to replace the flat space of Euclid. While this was intriguing, and led to a lot of complicated equations, to my way of thinking, it did not yield anything of great importance. The one significant item, the invariance of the speed of light, was of course highly significant, but this came out of the special theory of relativity, and could even be derived independently. The conclusion of the general theory - that light be bent more than predicted by Newton and that the perihelion of Mercury should advance a few seconds per century - seems small potatoes for such heavy investment. The mountain labored and gave forth a mouse.
More significantly, relativity was a misnomer: the theory was only incidentally a theory of relativity. Its true purpose was the search for invariants, i.e., absolutes: quantities which would be the same for all observers. It is this aspect of relativity that has had the greatest impact and has led to the present so-called cosmological postulate: the thesis that the universe, except for local irregularities, is the same for all observers. Right or wrong, this point of view is central to modern cosmology .
Moreover, relativity, as the search for absolutes, overlooks a very basic and important absolute, namely, rotation. (The reader may satisfy himself that rotation is an absolute by getting up from his chair, making a 360° rotation, and sitting down. If rotation were relative, he would be entitled to say that the universe had spun around him, and not that he had turned. But if he maintains this, then all the stars must have moved through space at velocities exceeding the speed of light. Alpha Centauri, the nearest star, would have had to move forty-two light years in the time it took him to turn around, that is, over a billion times the speed of light, and this possibility is barred by the theory of relativity. Therefore rotation is absolute and not relative.)
This question has not been overlooked; P. Bridgeman wrote a rather inconclusive book on the subject. Eddington too, in The Nature of the Physical World,* considers absolute rotation, but fails to recognize its importance for cosmology, or its ultimate connection with angular momentum, which he does show to be significant as an absolute. Momentum is relative, but angular momentum, based on rotation, is absolute.
In any case, my dissatisfaction with relativity fed my interest in the alternative theory that began to open up after I recognized the theoretical importance of seven-ness, which not only confirmed the possibility of seven stages to process, but cast new light on the old questions. In particular, the conflict between the continuum of relativity and the discreteness of quantum theory - a question with which Einstein had been concerned, but which he did not resolve. Einstein, in fact, could not accept the implication of quantum theory: "God," said he, "does not play dice with the universe."
*Eddington, Sir Arthur Stanley. The Nature of the Physical World: New York: Macmillan Co., 1937; Ann Arbor: University of Michigan Press, 1958.
The torus and individual existence
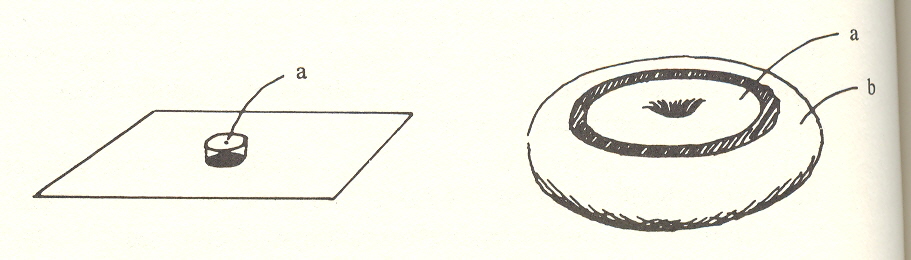
But I could see a way out. What the quantum theory established are the singularities within the space-time continuum: photons, protons, or electrons; these entities are quasi-independent point sources, islands of uncertainty (or of mass, it matters not). They are unique existences with a definite self-energy. My predisposition to analogies led me to see the problem of their existence as equivalent to the old problem of free will in a universe run by God: how can there be self-determined entities in the continuum? The solution was provided by the torus, which furnishes what is known as a different connectivity. In the case of a plane or the surface of a sphere,
a circle cut around a point a will completely separate it from the rest of the surface (1). In the case of the torus, a circle cut around a point need not necessarily separate it (2), for here, despite cut b, point a remains attached to the rest of the torus. So too, the self, in a toroidal universe, can be both separate and connected with the rest of the universe. And the problem is the same for many selves which would constitute more holes; a hole for each but all connected.
Meanwhile,
the evidence for seven stages to process found reinforcement from my study
of nature; in the case of atoms, the periodic table showing seven rows; in
the case of molecules, seven orders of combination, and so on. The
theoretical evidence also grew. To my great excitement, I discovered that
the formula for the volume of the Einstein-Eddington
universe, the so-called hypersphere, was 
the same as the
volume of the torus with an infinitely small hole!
Eddington discusses the hypersphere in his Fundamental Theory, in which he answers the question of the unification of quantum theory and relativity once and for all. (See Appendix III.)
Eddington explains that the new way of taking account of curvature is phase, and that phase space will constitute a fifth dimension at right angles to space-time.
Phase
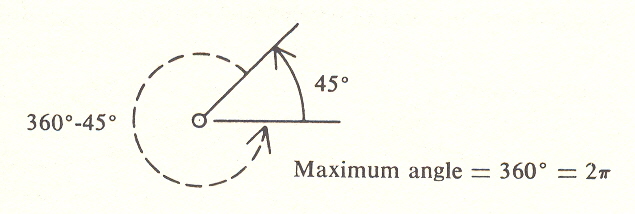
is, of course, angular relationship and has a range of 360° or 
*
because angle is measured over this range. It can be direction, or it can
be what I called timing in Chapter V, the lead or lag between an
input and a reaction.
*Strictly
radians where a radian is a radius laid out on the
circumference of a circle.
Since choice is expressed either as direction or as timing, it can be equated to the phase dimension. That is to say, if we want to assign a dimension to choice, the appropriate dimension would be angle. (The question of whether you vote with [in phase] or against [out of phase] is one of angle.)
To
carry the argument a step further, our uncertainty of what someone else
would choose would also be expressed as an angle, and the maximum
uncertainty as the angle . Quantum physics tells us that our
uncertainty in a given situation has the value h, a unit of action.
This unit, since it can be divided by
to obtain h bar, must
contain
and hence includes uncertainty of direction (as well as of
action).
This can be made clearer if we realize that, besides the limitations described by Heisenberg, observation is confined to its own cycle of action. For example, we hear a sound. If the frequency of the sound is reduced to much below 16 cycles per second, we no longer hear it as a sound; it becomes a series of separate beats or is heard as a rattle.
Contrariwise,
if we were counting beats and the frequency passed above 16 cps, we would
no longer distinguish separate beats; from that point on, we would hear a
steady sound, and be unable to distinguish fractions of a cycle. Our
measurement would be 
which in terms of cycle would be 
i.e., an uncertainty of
(as we've said, you might count
the
turns of the
corkscrew, but you wouldn't know where it ended up).
This uncertainty holds for all measurement, it being understood that the uncertainty is that of the observer while for the object it is freedom.
We now have the pieces of our puzzle and can put them together. We have two contending theories to reconcile, relativity and quantum theory. Relativity says that the universe or space-time is curved and continuous. Quantum theory says it is discontinuous. Relativity says that curved space-time might be spherical or it might be saddle-shaped.
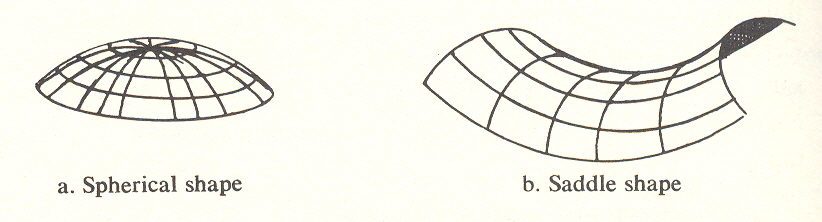
In one case, parallel lines converge; in the other, they diverge. Of the two, the latter is the more interesting. We say if space-time is to be continuous and saddle-shaped (say), then it cannot stop as is shown in the sketch because if it did, it cannot have a boundary without requiring a higher space in which it is imbedded. Therefore it must continue. What will we get if we fill in the part that is not shown?
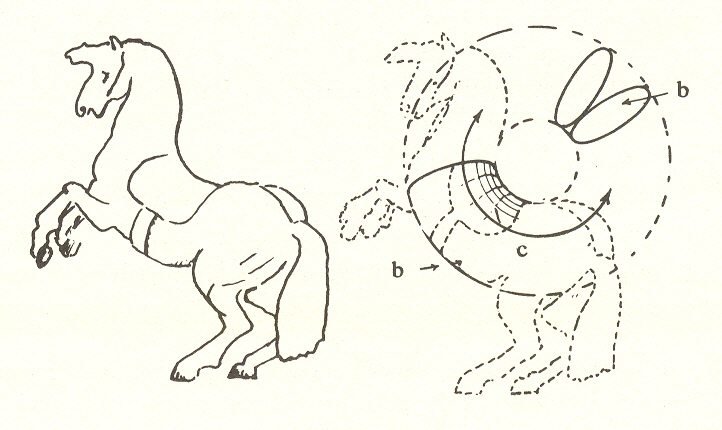
Thinking of the part of the saddle that goes around the girth of the horse and filling this in, we will obtain b. Thinking of the front and back continued in the direction of the arrows, we will obtain c. Thus the whole figure will produce a torus or doughnut of which the original saddle space is only a part.
Quantum physics and the control phase
What
about quantum physics? As Eddington pointed out, the curvature of
space-time can be replaced by the phase dimension whose measure is ,
and this
is the uncertainty inherent in quantum theory. In other
words,
Eddington recognizes that the curvature of relativity is the same thing as the uncertainty of quantum theory! But how about scale? Certainly the microscopic uncertainty of an individual proton is not the same as the vast curvature of space-time, which wouldn't "return" or complete its cycle for billions of years. True, but both have the same topology! Whether we deal with the particle or the universe of particles, the topology is toroidal;* their difference is in their time scale.
*This, incidentally, is the conclusion reached by James Archibald Wheeler on rather different grounds in Geometrodynamics, New York: Academic Press, 1974.
Returning
to the saddle space of relativity, it can now be appreciated that the
extension of the saddle which carried it around the girth of the horse,
and again in a vertical plane to complete a torus, constitutes two
circularities, two uses of 
and these two 
bring it
about that:
We therefore say that the hypersphere is a torus!
It is curious that this hasn't been recognized (I asked Dr.Wigner at Princeton about this, and he thought it had not been noticed). In any case, the torus and the hypersphere have the same formula, and the requirement that space-time be both saddle space and continuous can be met only by the toroidal figure.
The
next step is more drastic. We want to know what the extra 
means. We
know that it has to do with the cycle of action. That is, we know that
every entity, from atom to galaxy, has a cycle of action and this cycle is
represented by . But is this all? If we recognize that anything
physical expresses itself spatially as a
sphere - in the sense that a sphere
is the "shape" of a particle or it is the radius of action of a
fly or a man - and that the sphere has a volume 
we
cannot simply multiply this spatial existence by . The
product would
be 
which differs conspicuously from
Something
is wrong; we are off by a factor of 3/4. (Eddington discusses this
factor of 3/4, but since I
cannot follow his reasoning I will give my own and refer the reader to his
Fundamental Theory.) (See Appendix III.)
This factor of 3/4 is the most interesting of all. For it so happens that it is the 3/4 point of the cycle of action that has significance. Let us consider the different phases of the learning cycle, which is one example of the cycle of action.
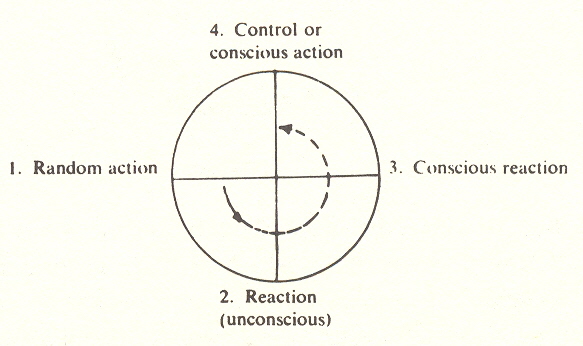
The start of the learning cycle is blind action: the infant reaches out at (1) and touches the hot stove, and at (2) reacts. Then at (3) he considers what has occurred; he becomes conscious that hot stoves hurt (if you are a behaviorist you can say he associates the pain with the stove), then at (4) he avoids the hot stove. This is the 3/4 point, conscious action, and merges back into (1) as avoidance becomes instinctive.
However,
it is the 3/4 point that is important. For this is the point of
conscious choice. It makes possible the "turn," first discussed
in Chapter V
and, as was there shown, its dimensions are 
(This
is the third derivative of position, i.e., change of acceleration or
control, the same control we use in driving a car. What we control is
force, for force is required to accelerate the car.)
but also:
In
other words, the extra
makes control possible. It is the entry of consciousness
into the universe. Its existence is borne out by the formula for the
hypersphere, by the extra uncertainty in the quantum of action (which does
not become control until it reaches the turn), and by Eddington's profound
recognition that the curvature of relativity is equivalent to the
uncertainty of quantum theory. We add that both are the capacity of
consciousness to act upon the universe, or to control determinism.
The seven postulates of projective geometry
These were the theoretical considerations that poured in upon me after I recognized that the universe and the creatures which inhabit it are toroidal. But while I now had plenty of evidence to show that the universe is toroidal, I did not have proof that the seven colors required to map the torus could be correlated to the seven stages of process.* It was the quest for this that made me sit up and take notice when, after Veblen's death, I read in an article entitled "A Mathematical Science"** that Veblen, in cooperation with John W. Young, had set forth the postulates (which they call assumptions) on which projective geometry is based. Projective geometry is the science that deals with the properties of figures as they are seen from different points of view by an observer; it is more general than ordinary or metric geometry, in which shapes do not change.
*See p. xxi and The polyvertons, later in this appendix.
**Newman, James R. The World of Mathematics. New York: Simon & Schuster, 1956-1960.
Ordinary geometry is based on four postulates, so imagine my excitement to discover that Veblen and Young had found that for projective geometry seven postulates were required:
I. If A and B are distinct elements of S, there is at least one class containing them.
II. If A and B are distinct elements of S, there is no more than one class containing them.
III. Any two classes have at least one element of S in common.
IV. There exists at least one class in S.
V. Every class contains at least three elements.
VI. All elements in S do not belong in the same class.
VII. No class contains more than three elements.
I immediately set to work to arrange these seven postulates in an arc. It was evident that they paired off in two sets, one saying "at least" and the other "no more than." Further, two dealt with one-ness (IV and VI), two dealt with two-ness (I and II), and two with three-ness (V and VII), leaving number III to do with combination for the bottom of the V (arc).
Placed in this manner, we can see that the postulates obey the rules of symmetry developed for the arc: one-ness, two-ness, and three-ness on the successive levels, with combination on the fourth, and the right-hand side inverting or reversing the left-hand side. There is even a resemblance in meaning, for the right-hand side, "no more than," exhibits a selfrestraint that contrasts with the "indulgence" of the left-hand side. This demonstrates a correlation between the postulates for projective geometry and the stages of process. We now need to show a correlation between the mapping problem and the postulates.
The polyvertons
To do so, we can begin by making a closer scrutiny of mapping. Mapping, by which we here mean coloring areas (countries) of a map in such a way that no two adjacent countries have the same color, seems a rather trivial subject, not entitled to the deep significance which attaches to topology which, as is well known, involves a more profound type of relationship than can be expressed in geometry.
But the coloring problem is not trivial. To realize this, consider the problem of the number of points that may be joined each to each by lines which do not cross.
As the reader may verify, no more than four points on a plane surface may be joined.
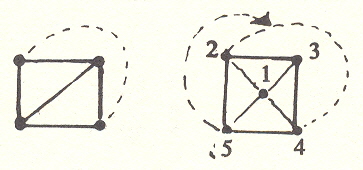
Five Points cannot. We cannot reach 5 from 3 without crossing a line.
This may seem no less trivial than mapping, for it is, in fact, the same problem in another guise, the line which joins two points being equivalent to a boundary between two areas and hence to a color distinction. Since coloring can be thus generalized, it can hardly be trivial.
Let us now impose the requirement that the lines must be the same length. We start with four points in a square as before:
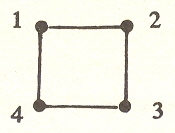
But the line 1-3, being a diagonal, cannot be the same length as the sides. In order for it to be the same, we must distort the figure, making in effect two equilateral triangles. But now we have increased the distance between 2 and 4. To join 2 and 4, we must hinge the triangles out of the plane of the paper and obtain a solid figure.
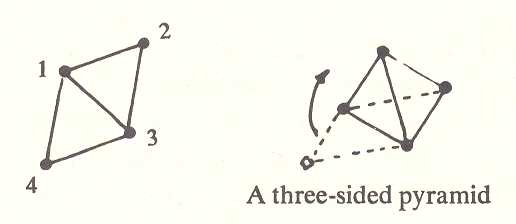
This is a tetrahedron. It has four vertices, six edges, and four faces. It is the figure which results from joining four points, each to each, with lines of the same length, and requires three dimensions.
In similar fashion, the equilateral triangle is the figure which results from joining three points with lines of the same length and requires two dimensions.
The unit line joins two points and requires one dimension, and the point, which stands alone, requires no dimensions.
We now have four figures correlating with four dimensionalities. The association with dimension makes it possible to recognize that these abstract entities have a resemblance to the powers of the first four kingdoms because they have the same number of dimensions as the kingdoms have constraints.
We can also recognize a correlation of the point to the potential power; of the line to binding, which ties things together; of the plane to form, which requires two dimensions to portray; of the solid to material objects, which combine form and substance.
But this is preliminary. We want to extend the method to deal with the higher dimensions and so obtain information about the higher kingdoms; the method of joining a number of points each to each gives us something to hold on to in this difficult area.
Beyond three dimensions
We now inquire: what happens when we join five points? Obviously, we
cannot do so in three dimensions without stretching one line.
We can join every point to every other point up to the last pair, shown in the figure as the vertical and internal diagonal 1-5. This line must be stretched.
Note,
of course, that this is not one of the regular polyhedrons. It has five
vertices, and apparently nine edges and six faces. But we are
forgetting the interior diagonal 1-5, which adds another edge, making ten
edges. This diagonal also contributes to three internal faces, which
along with the face 234, makes ten. These numbers are familiar. They are
the coefficients of an equation of the fifth degree, or 
We can see that the first 5 enumerates the vertices, the first 10 the edges, the second 10 the faces. What is the final 5? It is the number of tetrahedrons which can be obtained by selecting any four of the five vertices:
This alerts us to the fact that the point, line, triangle, and tetrahedron are also described by the coefficients of equations of lower degrees: this build-up of numbers is known as Pascal's triangle.
The correlation of coefficients to vertices, edges, etc., emphasizes the more abstract significance of these figures, and in addition, provides us with a quick way of knowing the number of edges, faces, etc., which becomes difficult for the higher figures.
What can we call these figures? Polyhedron, which means "manysided," is not the right word, since we would like to include the triangle, the line, and the point, which have no sides. But all the figures have vertices, so we may call them polyvertons. The figure having five vertices becomes, then, the pentaverton.
We noted that it could not be constructed in three dimensions without stretching one line. But since a stretched diagonal is an internal stress which implies storage of energy, we may correlate the pentaverton with the fifth kingdom, plants, for this is what the plant is able to do. So we now say a seed is a four-dimensional object (or five-dimensional if we have the zeroth dimension).
This promises to remove higher dimensions from their usual employment, which is impossible to visualize. We now have given concrete confirmation, for we can see a seed. It externally resembles any other solid object, say a pebble, but it contains an internal organization having the power to store and expend energy.
Joining six points gives us the hexaverton.
It has some resemblances to an octahedron, since it has eight exposed sides, each one an equilateral triangle. However, when we join all points we get fifteen edges. How many faces? The formula gives:
1 6 15 20 15 6 1
So there must be twenty faces and fifteen tetrahedrons (see if you can find them!).
Here we must have three internal diagonals,* each one stretched. This hexaverton correlates to the animal kingdom. The three stretched diagonals suggest the animal's power to change its shape by stretching in different directions, which is the basis for animal motion.
*1-6, 5-4, 3-2.
A further property of this model is interesting. Its description takes us back to mapping or its equivalent, joining points on a surface.
How may we join six points with lines that do not touch? This cannot be done on a plane surface, which is inadequate for more than four points. However, it can be done on a Moebius strip.
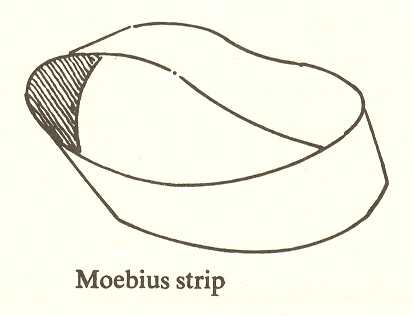
The tracing of the figure is facilitated by the convention of showing a Moebius strip as a square and remembering that the opposite edges join in an inverted fashion:
Note that the edge AB joins DC so that B touches C and A touches D
The right edge of the square is pictured as going around the back, twisting one half a turn, and joining the left. This twist makes it possible to join each of the five points to every other point. (The sixth point at the center is joined to all five which surround it.) Note that each point has five lines leaving it.
This seems quite different from mapping, but it is really the same problem. A map on the Moebius strip can be made which requires six colors.*
*Contrasted to the seven required on a torus, as we pointed out earlier in this appendix.
The heptaverton
Connecting seven points each to each requires twenty-one lines or edges. Starting with (1), we draw lines to the remaining six. We then join (2) to five more - it is already joined to (1) - and (3) to four more, and so on. So we have 6 + 5 + 4 + 3 + 2 + 1 = 21. We can confirm this from the coefficients, which are:
1, 7, 21, 35, 35, 21, 7, 1
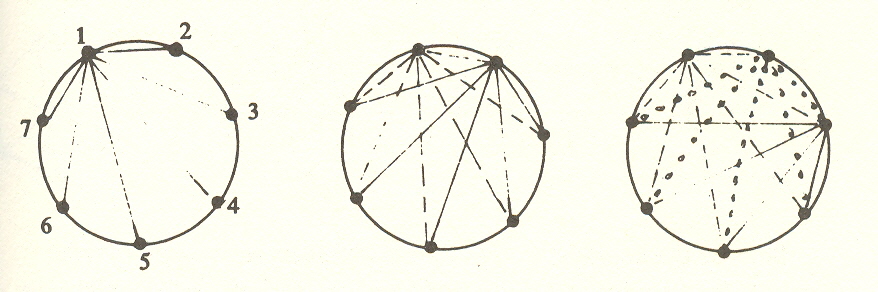
This figure can be thought of as adding a point at the center of the octahedron, and this additional point creates a set of six "compressed" diagonals in addition to the fifteen edges of the hexaverton, making twenty-one.
That this figure is the equivalent of the seven-color map is evident from the fact that seven points may be connected each to each on the surface of a torus with no intersections.
The demonstration is similar to that for the hexaverton on the Moebius strip, except that we now represent the torus as a plane whose opposite edges are imagined to curve around and join, top to bottom and right to left. Here there is no twist, but both pairs of edges join.
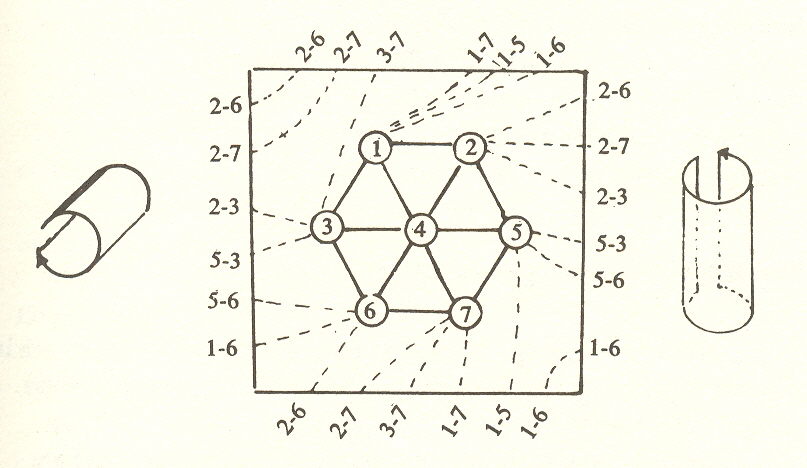
What is most interesting is that with the heptaverton we have the maximum possible number of triangles around each vertex. The tetraverton has three, the pentaverton four, the hexaverton five:
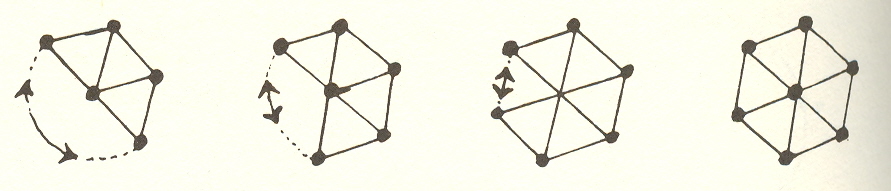
Since in the heptaverton each point connects with six others, the six resulting equilateral triangles fill up the 360° of space available in a plane. This suggests we can go no further.
A quite interesting paradox is suggested by the fact that space would be filled by the heptaverton. Suppose we were to make a heptaverton model of the universe. We would find that the interface between the model and the universe extended infinitely in all directions. And we would not know whether we were inside or outside the model!
While the vertons beyond the tetraverton (four points) are not possible in three dimensions of ordinary space and require the addition of imaginary dimensions, it would appear that joining more than seven points is impossible even with imaginary space.
This is given some credence by the progression we have encountered, first one, two, and three real dimensions, then one, two, and three imaginary dimensions.
Counting the zero dimensionality of the point, we have seven dimensions, and if these are all that are possible, we confirm the sevenfold nature of process.
Seven postulates compared to seven points
It is interesting that the problem of joining seven points each to each is in some respects equivalent to the postulates of projective geometry mentioned earlier in this appendix.
Veblen and Young show that the postulates imply that there are precisely seven elements or points in S (the totality), and that there are seven classes each of which contains three elements. They illustrate this by posing the problem of creating seven three-man committees from seven men, the committees to be chosen in such a way that no two persons are together in more than one committee (postulate II).
If the seven men are a b c d e f g, we may select the committees by taking a, b, and d for the first committee, b, c, and e for the second, and so on.
a b c d e f g
a b - d
b c - e
c d - f
d e - g
e f - a
f g - b
g a - c
This can be shown for the seven points of the heptaverton thus:
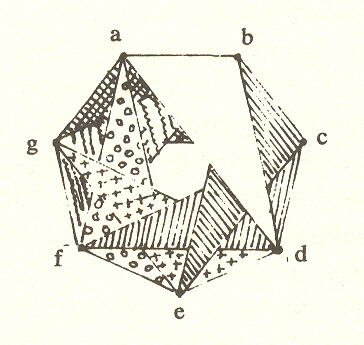
There are seven triangles, each of which contains three points, such that no two points are in more than one triangle (or no two triangles share an edge). The seven triangles use up all twenty-one edges of the heptaverton.
The "classes" of the postulates are thus faces, each one determined by three points.
We can also show that there are seven tetrahedrons with no face in common.
Veblen
and Young prove that if two universes 
satisfy the seven
postulates (in that their elements and classes correspond), then
are abstractly equivalent, and constitute the same universe. They entitle
the set of postulates which lead to such isomorphic examples categorical.
We have shown that the heptaverton is:
1. Isomorphic with the torus, in that the connections of seven points with lines which do not cross is equivalent to mapping seven countries. (This is also stated by Hilbert.)*
2. Isomorphic with the seven postulates, in that both their elements (points) and classes (triangles) can be placed in correspondence.
Therefore, since both the torus and the seven postulates are isomorphic to the heptaverton, they are isomorphic to each other. We could therefore conclude that the seven postulates require a toroidal universe.
However, this is not our goal. We want to show that the seven powers, as charted on our grid, are isomorphic to the torus, and this requires that the powers be isomorphic to the postulates.
It should be sufficient to show that the powers can be assigned in one and only one way to the postulates. Since the powers are cumulative, they have a necessary order which of course is that of the kingdoms of nature. We have shown that when the postulates are placed in the order shown on (See The seven postulates of projective geometry earlier in this Chapter), they correspond to the powers, and preserve the same symmetries. This ordering placed the postulates "at least" on the left (what comes first) and "no more than" on the right (what follows). This is necessary since we cannot limit the membership until it has been filled. The ordering also places postulate IV (there exists at least one class) first. This is the only postulate that could come first, because it establishes existence. Postulate I must follow because it distinguishes two things, and V must come third because it deals in three. The ordering of the last three is determined by the symmetry.
We can thus conclude that the powers have the property of the postulates, and are categorical. Moreover, it follows that any universe, by which we imply any process, must imply the same powers.
Here we must recognize that the description of the powers is subject to considerable flexibility. In a sense, the powers are undefined terms. In another sense, they are not. Their proper definition requires only that:
1. They be independent and categorically distinct.
2. They be cumulative (which implies a definite order).
*Hilbert, D., and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea Publishing Co., 1956.
These requirements can also be met by distinctions based on dimensionality (i.e., one-ness, two-ness, etc.), which, it will be appreciated, imply degrees of freedom and hence levels (as in the arc).
We are thus equipped with a paradigm that can be enforced as a categorical principle.
The reader is likely to object and say that this violates the principles of valid inquiry, which should be based on the inductive method.
But this misses the whole point of our method. A true scientific inquiry must be based on some paradigm, and if this is not recognized the paradigm remains unconscious. Such is the fourfold paradigm which structures "objective" science and leads to determinism. It is false because it overlooks first cause and makes rationality the final arbiter. Its emphasis on objectivity omits the projective aspect and leads to a cul-de-sac. It fails to discover the reflexive quality of the universe. The sevenfold paradigm corrects these errors and opens the closed system that the fourfold would dictate. It frees us from a misinterpretation of the constraint of law.
Approaching a subject with the sevenfold paradigm can be compared to approaching a machine with a knowledge that, in addition to its structure, it has a purpose and can be turned on, whereas the objective paradigm would permit only a study of its structure.
Importance of the committees
The committees, or subsets of three points, are important because they meet the requirements of the postulates of Veblen and Young. We have shown that the postulates can have a correspondence to the seven kingdoms.
We are entitled to extend this correspondence and ask, "If the postulates correspond to the kingdoms, what do the committees correspond to?"
Clearly, the committees must be interactions between kingdoms - or perhaps better - between the powers of kingdoms.
But my effort to discover such correspondence was not successful until I discovered that the committees could be constructed in a different way from the one already shown.
For example, instead of the connection in Fig. 1, we may connect the points as in Fig. 2.
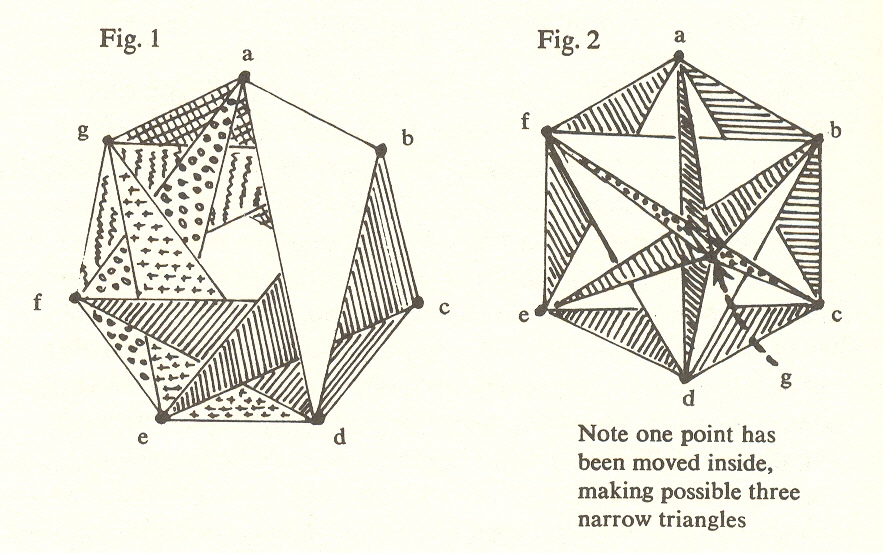
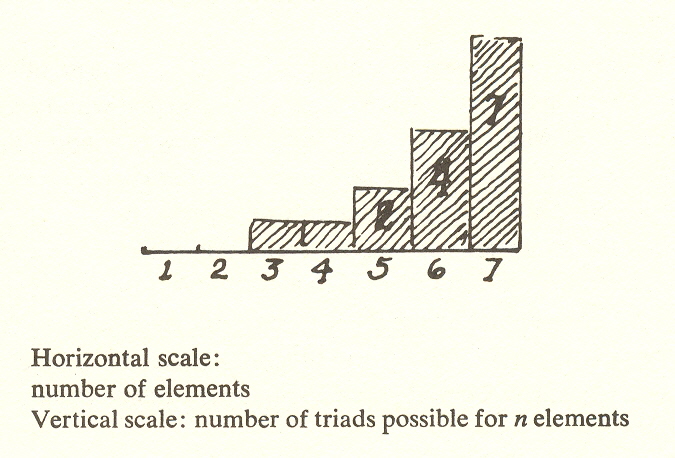
But this was still not fruitful. What did prove fruitful was to recognize that the formation of committees is cumulative. As the number of elements increases, the number of committees does too, but more rapidly, and drops to zero after seven. (After seven it becomes impossible to comply with the postulate that any two committees have a member in common. )
Number of elements 1 2 3 4 5 6 7 8
Number of committees 0 0 1 1 2 4 7 0
Taking six points, for example, two more committees become possible when the sixth point is added.
At this time I was working on the material in the chapters on evolution and had drawn the three diagrams shown at the end of Chapter XII, to represent three types of evolution. I then realized the three kinds of evolution were committees - reinterrelationships between the powers of three kingdoms.
Since there are seven committees, and only three types of evolution, I had four triangles (or committees) unaccounted for. But the problem was simplified by the fact that having filled in the three evolutions, there was only one way to draw the remaining committees, keeping in mind that the first committee consisted of light, particles, and atoms - since this committee would come into existence first. The next committee, in addition to the two evolutions, is not possible until animals, and this committee interrelates cellular organization, animals, and light. I suspect it has to do with the introduction of choice into animals - and choice must have its origin in the free orientation which characterizes light. Surprising to me was the fact that I could not get a committee made up of plants, light, and molecules, which I thought would fit the storage of light by chlorophyll and hence be necessary to the plant kingdom.
The two remaining committees which come into existence with the seventh kingdom are (1) dominion, form, and animation, and (2) dominion, energy, and organization. Both seem to describe distinctly human activities, but I find them hard to distinguish. The animation of forms suggests mechanical gadgets - but so does the organization of energy. So I will have to consider there is more to be discovered.
However, the recognition of the cumulative factor uncovered more evidence for the uniqueness of seven. We have already noted the build-up of committees, which we will now call triads.
In addition to triads, it is possible to have tetrads (four-element subsets). These must have no more than two elements (an edge) in common. As with triads, this requirement cannot be met with more than seven elements.
In the case of the tetrads, there is an even more rapid build-up.
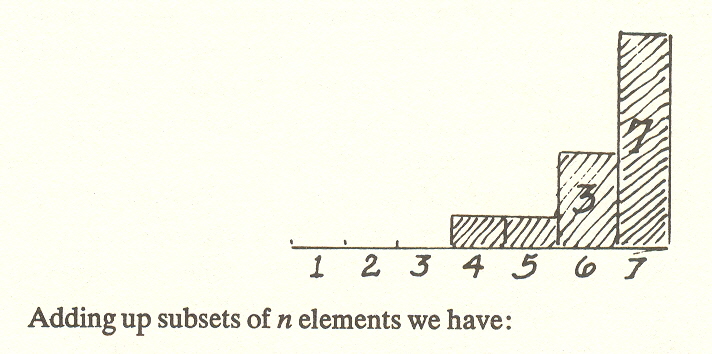
Adding up subsets of n elements we have:
In short, then, the number seven is unique in that it contains the maximum number of possible subsets - more than twice as many as any other number. It is also the largest number for which linked subsets are possible.
The uniqueness of seven is thus confirmed. There is no other number which has as many subsets. It is interesting also that while we do not at present know what these subsets "mean" or how they apply to practical questions, we believe them to be interactions between powers - and hence important to the understanding of cosmology.
Since the importance of subsets does not begin until the fifth kingdom or stage (this is the first kingdom to have two three-element subsets), we might suspect that one of these subsets had to do with evolution because this is where evolution in the usual sense of "survival of the fittest" begins. However, this conclusion was reached independently in Chapter XII.
But why have subsets been overlooked in the exact sciences? I believe the question answers itself. The exact sciences cover only the first four kingdoms in which the notion of subsets is not appropriate (since there is at most only one subset of each kind in a kingdom).
We have thus confirmed, from considerations of the most abstract sort, the uniqueness of seven.
