*
THE ROOTS OF UNITY
Negative and imaginary numbers
I will now venture into another discipline, algebra. The use of negative and imaginary numbers in algebra confirms the fourfold nature of analysis, and also provides additional insight into the threefold. Here again, I should acknowledge that I am using the concepts of a discipline for purposes outside their usual application, but there are certain discoveries of mathematics which make valuable contributions to our study.
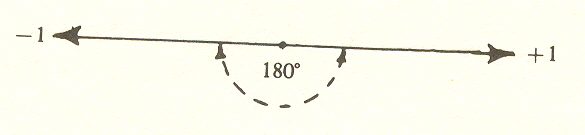
The evolution of mathematics was given great impetus by the discovery that it was possible to use negative numbers, negative quantities. If we represent positive numbers extending to the right of zero, we can represent negative numbers extending to the left:
etc. . . . -3 -2 -1 0 +1 +2 +3 . . . etc.
With this device, we may describe addition as moving to the right, and subtraction as moving to the left. This makes it possible to subtract a larger number from a smaller one; for instance, if we take 3 from 1, we get -2, which is a real (although negative) quantity.
Another important concept was that of imaginary numbers. They were not so much discovered as encountered.
Mathematics had arrived at the concept of a number as having roots; numbers which, multiplied together, will produce that number. When the concept of negative numbers came along, there was a clash. What would be the two numbers which multiplied together would produce a negative quantity, -1, for example? For a time there was no answer. The square root of a negative quantity must be impossible. So it was called imaginary. But when Gauss, called by Bell the prince of mathematicians, found a method for representing imaginary numbers, it was not long before their value was appreciated, and today they are just as important as real numbers. This method uses the Argand diagram, which, in essence, correlates unity to the circle, and roots of unity to fractions of the circle.
Recall that negative numbers were pictured as extending in a direction opposite to positive numbers. In this way, the square roots of unity, +1 and -1, can be expressed as the opposite ends of a line with center zero. This line can be thought of as an angle of 180 degrees, or a diameter.
Gauss
extended the idea further and pictured 
as halfway between
+ 1 and - 1, or an angle of 90 degrees from the line -1 and +1. Thus, if the division of unity into plus and minus is a diameter, or 180 degrees, a second division leads to an axis which "mediates" this diameter, or an angle of 90 degrees.
Thus we have two axes - the horizontal representing positive and negative real numbers, and the vertical representing positive and negative imaginary numbers. These two axes form the complex coordinate system, and a number on the plane described by these axes is a number having a real part and an imaginary part.
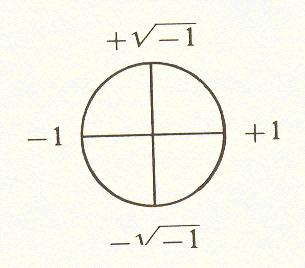
Using the Argand diagram, this circle of unit radius (radius = 1) on the complex coordinate system, the other roots of unity (cube roots, fifth roots, etc.) are found simply by dividing the circle into three, five, etc., equal parts. Finding the roots of unity becomes simply a matter of inscribing polygons within the unit circle: a triangle for cube roots, a pentagon for fifth roots, etc. The roots are the points on the circle; their values have a real part and an imaginary part, and are measured along the horizontal and vertical coordinates respectively. This means that they are measured in terms of square roots and fourth roots.
From this extremely powerful simplification, it follows that all analysis is fourfold - any situation can be analyzed in terms of four factors or aspects. This not only confirms Aristotle (his four causes) but explains why quadratic (literally, "four-sided") equations occur so frequently in mathematics.
But the important generalization that all analysis is fourfold works both ways. It shows both the extent of the fourfold and the limitations of analysis, for there are things in the content of experience that are beyond analysis.
Staying within the geometrical method already set up, we can show that these non-analytic factors involve three-ness, five-ness, and seven-ness. Despite the fact they can be described analytically, this description fails to capture their true nature.
Cube roots and the threefold operator
As I said, we can express the cube roots of unity analytically in terms of square roots; that is, using the two-dimensional diagram.
These
roots are obtained by inscribing an equilateral triangle within the
circle. One of these roots is +1; the other two are points half a unit to
the left of the vertical diameter, and half a side (of the triangle) above
and below the horizontal diameter. Since the side of the triangle is 
,
the vertical coordinates are
the
i being used to
indicate that we are measuring in the vertical direction. (The imaginary is
commonly represented by i.)
By this we see that the values for the cube roots of unity can be expressed as square roots.
But
is an irrational number, meaning that it is not a
ratio of whole
numbers.
Since 
is the diagonal of a unit square,* we
might expect to
find some expression for
in units. We need not look
far to find what
this is, for
is the diagonal of the unit cube.**
* A unit square is a square whose side is 1.
**A unit cube is a cube whose side is 1.
So
in order to represent
in unitary fashion,
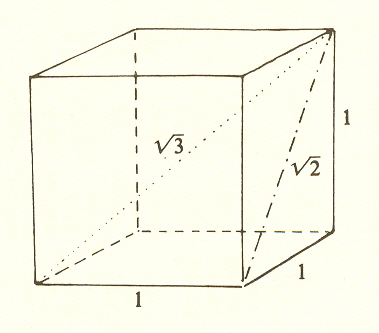
we must leave the two-dimensional plane. Full representation of the cube roots of unity ultimately involves the three dimensions of space. The threefold operator, represented analytically as equidistant points on the circle, is actually a three-dimensional activity, whose measure gives only its analytic aspect. The analytic aspect, which is in two dimensions, does not convey the full meaning of the cube root; it is like the shadow of a solid figure.
The threefold nature of the cube root is nonanalytic. It involves categories which differ from one another more profoundly than those of the fourfold.
Here we have a formal device to show the inadequacy of analysis for a complete account of the world. This is but one example of the fundamental distinction between the threefold and fourfold operators, a distinction so important to our theory and to life that I will devote the next chapter to a comparison between these two operators.
