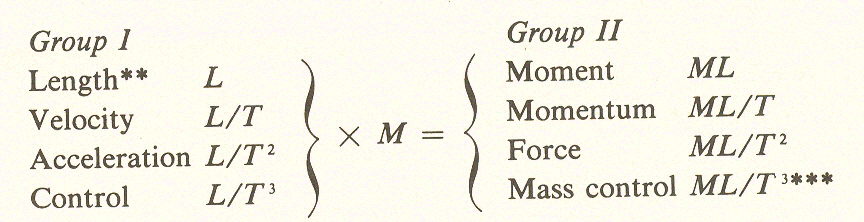
*
GENERATING OTHER MEASURE FORMULAE
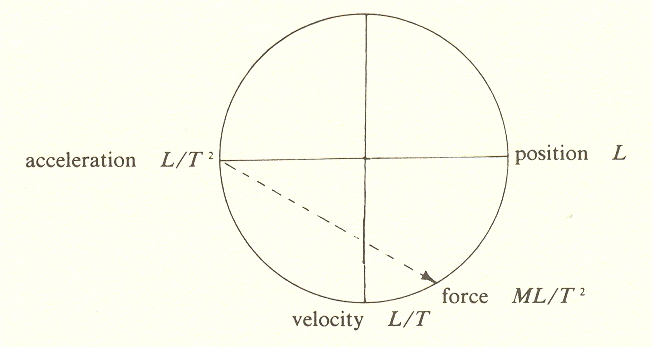
In Chapter II, we noted that position and its derivatives, velocity, acceleration, and control, are measure formulae. But there are other measure formulae to which we should now give attention. In the pursuit of meaning, the measure formulae are invaluable because they replace words. Words depend upon definitions, which in turn depend upon other words, making a closed circle. The measure formulae, as we have seen in the case of length (L) and its derivatives, are more explicit than words in that they define operations, like the operation of the derivative. Thus they anticipate the aspects or categories that we may expect a situation to have. Automorphic operations are operations which, when applied, repeatedly return one to the start after a certain number of steps. Thus the operation of turning through an angle of 90 degrees when applied four times returns one to the start. Similarly, negation is a two operation because the negative of negative (double negative) is positive.
The measure formulae are the outcome of centuries of struggle on the part of physical science to arrive at a set of terms that can be formulated in such a way as to leave no vagueness, no ambiguity.* They describe the skeletal anatomy of all of science, and even anticipate modern discoveries.
*For an excellent description of these struggles, see Jammer, Max, Concept of Mass. Cambridge: Harvard University Press, 1961.
Quantum theory, in giving prominence to the quantum of action* as its most basic ingredient, only drew attention to a concept already included in the measure formulae.
*Not to be confused with the cycle of action, as we shall see shortly.
The measure formulae we have considered - position and its derivatives - are given in terms of two variables, length (L) and time (T). These two variables, more correctly referred to as parameters, together with a third, mass (M), are the basic ingredients of physics, more basic even than the formulae, as they are fewer in number; the formulae are combinations of these parameters. M, L, and T have the same status in physics that points and lines have in geometry; they are the "undefined terms," the fundamental ingredients from which all the measure formulae are constructed.
The formulae we have considered so far do not involve mass. If we multiply each of these formulae, length and its derivatives, by mass, we get a second set of measure formulae:**
**Position was our earlier term, but here we use length because it is the measure of position.
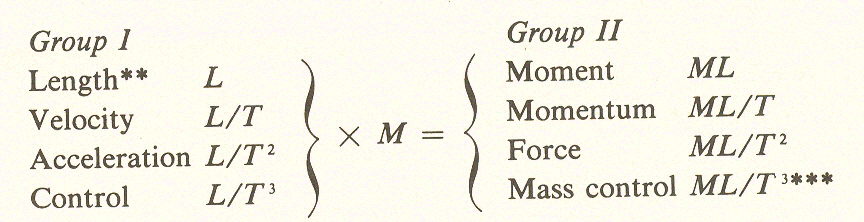
***Until recently there has been no conventional word for the third derivative of momentum. It is now recognized, however, and used in aeronautical engineering, where it is called power control. I would prefer to call it mass control (material extent of control).
By multiplication of a new parameter M, we have obtained a second set of four measure formulae. If we now multiply the second set by L, we will obtain a third set of formulae:
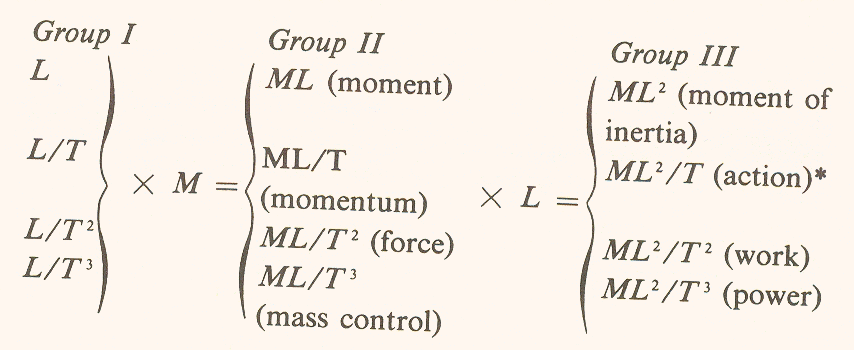
*The
term "action" here is not to be confused with the "four
kinds of action" in group I. This term, 
is rate of
change of inertia.
These
twelve formulae include all of the ten used to analyze the dynamics of a
moving body, plus two
not presently
recognized in physics textbooks, but used in engineering.
Formal device for "reducing" M, L, and T
In the physical sciences, M, L, and T are considered basic, that is, not capable of further reduction. In our search for the origin of meaning, however, we are interested in the possibility of reducing them to the even more basic unity or totality. We have already reduced a total situation (the cycle of action) into its four aspects by operation of the derivative. In the cycle of action, and in each of the other groups shown above, the operation of T (time) resulted in a division into four. T, then, may be considered as one-fourth of unity: it quarters the whole.
If we want to reduce M and L to aspects of the whole, we need similar conventions for representing them on the diagram. What part of totality is M?
I will not take the time here to conduct the reader through the process of trial and error which finally convinced me that M is 120 degrees.* My clue was in the threefold cycle, where the shift from act to result may be seen as equivalent to embodiment or incorporation (thus "massing") - literally, as in eating a meal, and also metaphorically, as in the accumulation of experience. Action X mass = result.
*One
hint is that mass is volume times density, Since volume is 
and density is a number equivalent to another L, we can suppose
As
we shall later show, L = 30 degrees so M = 120
degrees.
Since division (or differentiation) in the case of T was represented by clockwise rotation, multiplication (or integration) should be counterclockwise:
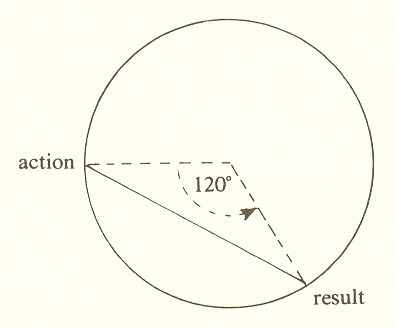
Using this device, representing multiplication by M, we may transpose to the diagram of the fourfold:
Then we may set down the remaining group II formulae on the circle representing totality.
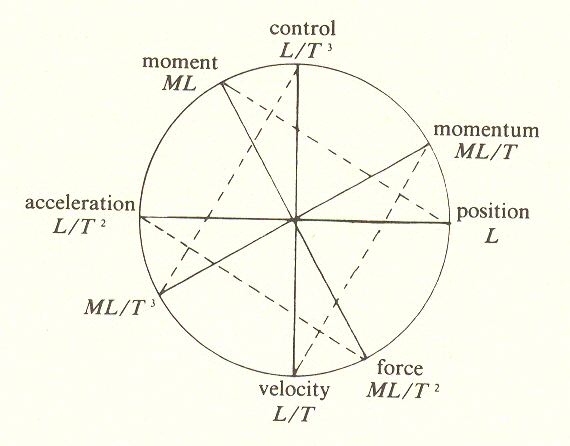
The placement signifying multiplication by L is not so difficult, because there are now only four spaces remaining on the diagram for the four formulae in group III. Of the four available spaces, only two (30 degrees and 120 degrees) would divide the circle an integral number of times. And since 120 degrees is already used to represent M. this leaves 30 degrees, or one-twelfth of the circle, to represent L.
By putting in the formulae of group III at 30 degrees from their corresponding group II formulae, we have completed the diagram of totality in terms of M, L, and T.
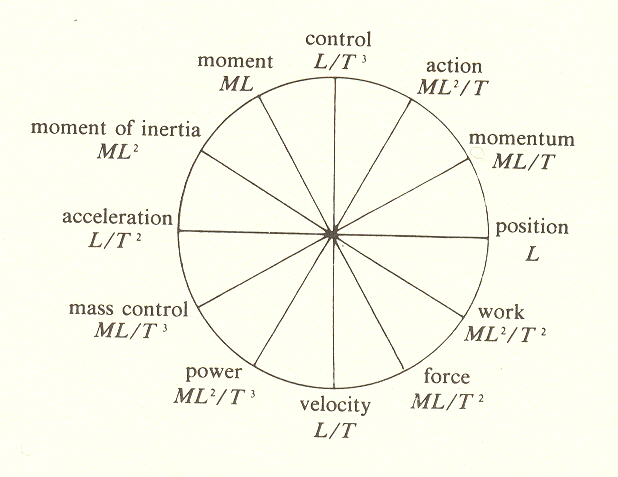
Here, then, is the division of the whole into three and four parts, referred to in the Introduction. (We will not deal with the twofold division until later.)
When I first attempted to find a division of the whole into parts, I tried to make these divisions M, L, and T, plus one more to be discovered. But this did not work, and finally it became clear to me that M, L, and T are three different ways by which the whole is divided: by T into four parts, by M into three, and by L into twelve.
These discoveries, as I have attempted to show, were accompanied by the recognition of angular relationships between the different fundamental terms, the measure formulae.