*
DERIVATIVES
Derivatives are the basis of the calculus discovered simultaneously by Newton and Leibniz and are the foundation of the science of motion. A derivative with respect to time is a rate of change. Thus, velocity is the rate of change of position with respect to time-represented as L/T, miles per hour - where L designates distance and T designates time.
The second derivative, acceleration or rate of change of velocity, is
. My Volkswagen can accelerate to sixty miles per hour in ten seconds. Note that we divide by time twice: first in miles per hour, then again in mph per ten seconds.
It is very interesting that distance and its derivatives are known to us through different faculties. We know position directly through the senses; we know velocity by computation. (The fact that the earth is moving through space at fifteen miles per second is only known through observation and careful computation with respect to the distant stars.) Acceleration, however, we know through feeling. We feel ourselves pushed to the side when the car goes around a curve, or thrown forward when we make a quick stop.
Are there any further derivatives? In his book Differentiation (1969), P. P. Korovkin writes, "In Newtonian mechanics v [velocity] and a [acceleration] are key quantities, but da/dt [the next derivative] plays no role at all." The official line, in other words, is that further derivatives, though theoretically obtainable, are of no importance. But let us examine this assumption. The next derivative would be change of acceleration. It is by change of acceleration that we control a car - by applying the brakes, pushing the accelerator pedal, or steering. These are all methods of changing acceleration, i.e., "driving" the car. We say we drive the car; actually it is the engine that "drives" the car, but we control the engine.
The third derivative, or change of acceleration, is not mentioned in physics textbooks, this despite the fact that it is the basis for the science of cybernetics. It is mentioned in advanced control system texts, and there are courses given in "control" in today's colleges, but the idea of the third derivative has not penetrated physics or philosophy. It is in regular use in aeronautics under the title "jerk," an unfortunate term based on the operation of black box control systems that are either on or off and hence not representative of the more gradual or continuous control we exercise in life - not only in cars, but in our every motion. While we sense position, compute velocity, feel acceleration, we do control.
Why is control, the third derivative, not mentioned in textbooks? How does it come about that we have a vast technology, an industrial age, based on manufacture and use of controllable machines, with no mention of control in theoretical physics?
One might say that the mindset that ignores control may be aesthetically inspired by a need for a world regulated by exact laws. Historically such aestheticism has had a strong appeal, especially for the scientist engaged in the search for objective truth. He must study nature impartially and investigate how it behaves when left to itself; when he weighs an object he must not put his hand on the scales. Therefore all laws are predicated on the assumption that energy is not being added to or subtracted from a closed system, and in this way the regularities of nature are discovered - laws of motion, laws of gas pressure and temperature, etc. The scientist is understandably impressed with the remarkable consistency that emerges and with the predictive power that rewards his labors.
Yet, having found that under these special conditions matter behaves in this remarkably precise and orderly fashion, the theoretical scientist tends to disregard the fact that he had assumed for purposes of his experiment that no energy was added or subtracted from outside the system, and he concludes there can be no addition or subtraction to mar the predictability and order. It does not occur to most scientists that the existence of the third derivative makes possible just this addition or subtraction of energy. To the mind directed at the discovery of a world order, the mind trained to avoid human intervention or bias of any sort, it is abhorrent to turn traitor to this beautiful creation. Unable to put it to use, unable to take advantage of the knowledge of law so obtained, the scientist becomes the chef who has created such a marvelous cake he cannot bear to eat it.
Thus it is that the sharp line is drawn between technology and science. Technology, driven by invention, does not hesitate to eat the cake or use determinism. This is precisely what technology does. By using nature's laws, it creates products, and when these products are machines, it takes for granted that the machines can be controlled.
Control and Life
In this reference to use and control, I am assuming that the third derivative is kept optional. The scientist would admit that a planet in an elliptical orbit changes its acceleration. When the planet is close to the sun, the acceleration is greatest, when far from the sun, the acceleration is least. So there is in this case change in acceleration, but the acceleration varies inversely with the square of the radius, and is therefore linked to position; it is not open or optional. The elliptical orbit, then, does involve the third derivative, but this is a special case.
The governor of a steam engine or a thermostat that has been set to a predetermined temperature are also special cases. The general case, however, allows control to be optional, subject only to the limitations of the machine. (We could not expect a 40 hp car to accelerate with the rapidity of a 300 hp car.) It allows the householder to reset the thermostat, the engineer to regulate the governor of the steam engine, and so on.
I emphasize the importance of the third derivative, or control, not only because it puts determinism in its place as the servant of free will - but because it lays the basis for a true science of life. The fact that man can control machines enable us to recognize that he also controls his body. Even to stand up requires the continual, but largely unconscious, exercise of control. And if man controls motion, as I said before, so, too, can animals control their motions, and plants control the chemicals to store energy and promote growth.
Here, at last, life enters the picture. Hitherto life has had no place in the scheme of determinism. Determinism is a dead picture, a portrait of inert matter obeying fixed laws, of dead planets repeating their monotonous revolutions. But with the expanded formalism permitting the addition of control, we can account for life. We realize that nature creates creatures who, through control, use the laws of nature for growth and self-maintenance.
Our problem here, however, is mathematics, and the need to challenge that curiously perverse view of mathematics, at once romantic and irresponsible, that declares that because mathematics is a pure science it has no bearing or obligation to the real world. Let us now try to see how this idolatry of formalism has obscured the very thing that could save science.
Higher Derivatives?
In Chapter 5 of his book Wholeness and Implicate Order (1980), physicist David Bohm gives examples of motion of increasing complexity: first, motion in a straight line; second, motion in a uniform curve; third, motion in a spiral. He goes on to say that there are higher and higher orders of complexity, which can be described by higher and higher "degrees of order," equivalent, I would claim, to the derivatives. (A point represents position, a line velocity and a curve acceleration. The spiral, change of acceleration, is control.) According to Bohm it would ultimately be possible to describe even the random motion of Brownian movement, not as disordered, but as involving an indefinitely high "degree of order."
But Bohm overlooks the fact that once we reach the third derivative, or control, the one which changes the uniform curve to a spiral, we have reached the point of option or choice. Thus, through control, we can produce any spiral, steer the curve back to a straight line, or introduce whatever new changes we wish.
Let us examine the implications of this. If there were higher derivatives, or paths that required them for analysis, and you were operating a vehicle and had access to these higher derivatives, but I did not, then you could move in a path that I, equipped with control of a similar vehicle, could not follow. But such is not the case. You, possessed only of control, can move in any path you please (subject to the maneuverability of the vehicle), and I, with a similar vehicle, can follow you. Following is subject to lag and may fail, but not because of a different derivative.
This being the case, further derivatives - i.e., derivatives beyond the third - are superfluous.
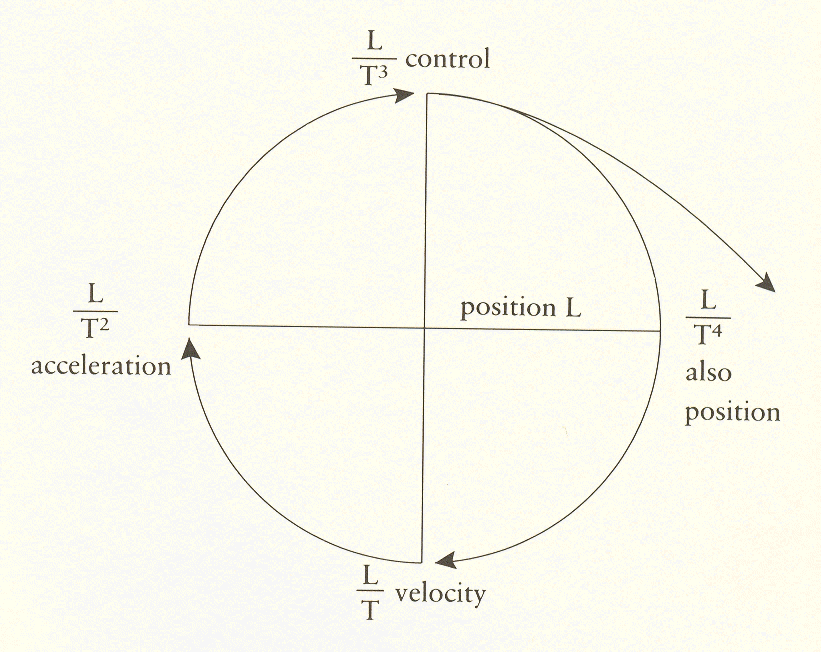
We may illustrate the sequence of derivatives and their contribution by the number of photos of a moving vehicle we would have to take to know its position, velocity and acceleration:
Let us take the case where there is a fourth derivative, that is, something that governs control. As we said before, control in the general case is optional. But as in driving a car, we can have a definite destination. This "governs" our control in the sense that when we reach the destination we stop the car and get out; or if we were bombing a certain target, we would guide the airplane accordingly. Again, in process control there is a product assessment, i.e., quality control.
So from this we can conclude that the target, be it a place or a quality of product, is the fourth derivative - the one that governs our otherwise optional control. But a target or destination is a position, and position is what we started with. Velocity enabled us to change position, acceleration to change velocity, control to change acceleration, and position to govern control. So we have come back to the starting point after four steps:
This is what is called a four operator, and it tells us that position and its three time derivatives are all the time derivatives there are; after three the derivatives repeat.
Now I do not take Dr. Bohm to task for his misunderstanding of derivatives to establish his thesis (that there is hidden, or implicate, order). The responsibility must be charged to mathematics, which just doesn't bother to inform us that the third derivative is optional - that is, it is inherently unpredictable. As I said, I do not deny that in some cases it is linked to one of the other derivatives (ideally, as in the governor of the steam engine, to velocity), but such cases are "degenerate" - that is, they do not permit full scope to the function.
Perhaps mathematicians would insist that the nature of the third derivative does not concern mathematics. But if that is their claim, whose concern is it? Certainly not the physicist's, who would not dare to question mathematics. Physicists often refer to Poincare's dictum to the effect that there is a theorem in mathematics that says if we know the value of a function and that of all its derivatives at a point we can predict the value at all other points.
The theorem in question, the one invoked by Bohm, is the Taylor series, which is very useful for finding the value of the sine or cosine of an angle. But the "function" in this case is a mathematical truism, a form of expression; it is not a statement about the physical world.
Since neither the physicist nor the mathematician recognizes that the third derivative is option, perhaps in the game they play "option" is out of bounds and cannot be mentioned. If so, they are not to be trusted with cosmology, which cannot exclude option because option is built into the same formalism that made science possible, the calculus itself.
The Implications of Mathematics
To sum up, then, we have seen several ways in which mathematics has to be called to task for failing to appreciate the implication of its own formalisms.
Thus, the custom of making use of n dimensions, irrespective of the value of n (a custom encouraged or inspired by the fact that the process of addition or multiplication is not affected by the values of the numbers added), is open to criticism. The three dimensions of space cannot be dismissed as a mere "special case" - three may be the only number of dimensions that a manifest world, an actual world, can have. And the question of how many dimensions a world can have, if not a question for mathematics, is a question for a higher authority, a science yet to be established from which mathematics would take its authority.
Again returning to the question of the degree of equations, mathematical formalism blindly assumes that the degree of an equation (the exponent of the unknown) can have any value. But a further inquiry shows important differences between linear and quadratic equations, and the fact that equations of higher degree become increasingly insoluble and have decreasing applicability raises questions: Is there or is there not a limit to the degree of an equation? And of what pertinence are equations that are insoluble?
Related to this is the unstated assumption that logic is limited to entities that have identity. Logic takes for granted that a = a. It would be foolish to try to deduce that if a = b, and a = c, then b = c, if one could not assume that a = a, notwithstanding the fact that each time I write a, I use different ink and form the letter slightly differently.
Such a consideration would probably have been regarded as trivial in any period prior to modern physics, where the issue of identity has been clarified by the discovery that the ubiquitous electrons and protons that make up all matter have no identity. There is no way to tell whether an electron leaving an atom is the same electron as the one that entered the atom. This is not a mere quibble, it is an important ontological principle. Identity, which makes separateness possible, only emerges at the next level of organization, when atoms themselves are formed. When the atom enters into a combination with another atom to form a molecule it changes only its outer electrons; its nucleus remains unchanged. This permits the atom to retain its identity when the molecule is broken up. (If this problem of something without identity still seems difficult, take comfort in the fact that the egolessness of things is a central teaching of Buddhist and Hindu philosophy.)
With the derivatives we have even more evidence that the formal procedures of mathematics blind us to important distinctions. In principle it is assumed there can be any number of derivatives. In principle, too, the derivatives are assumed to have no inherent properties that would distinguish one from another. But as we have shown, the time derivatives are known through different faculties, sensation, intellect, etc, and the third derivative, in the general case, is open or optional. If the third derivative is known or fixed, differentiation exhausts its repertoire and reduces to a four operator. This again indicates a responsibility in mathematics either to attend to the meaning of its blind formalism, and to admit that its own formal procedures are open, as it were, on one side, or to admit there can be a science of higher authority than mathematics.
Here again we find a parallel in logic in the Goedel paradox, mentioned earlier, which proves by logical methods that logic is incomplete.