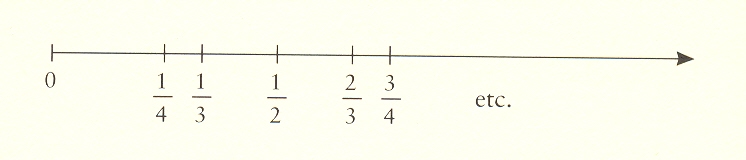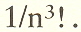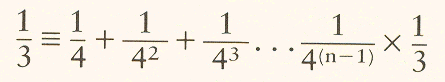*
CANTOR'S
INFINITIES
Arthur
M. Young
In
the late nineteenth century, Georg Cantor devised what was considered a
formal system for dealing with infinity. His system defined the infinity
of natural numbers, and contrasted it with the infinity of the
continuum. To do this he first developed a method whereby the rational
numbers (fractions) could be counted, i.e., put in one-to-one
correspondence with the integers:
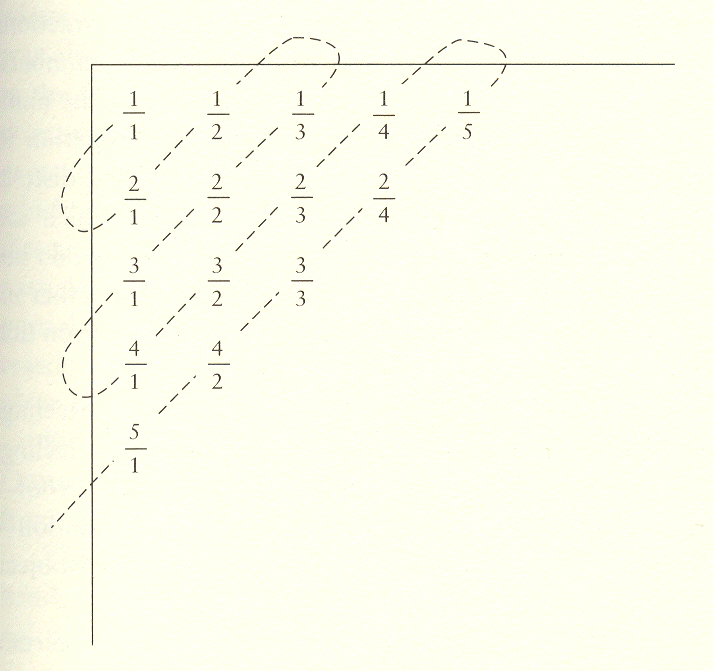
He
then placed the rational numbers on a line representing the continuum:
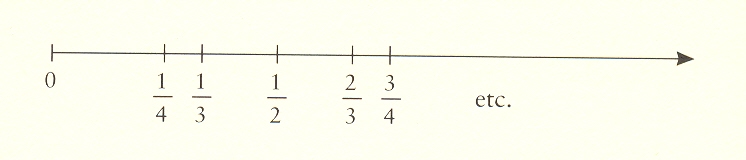
Cantor
next said that there must be many more points, points
that correspond to the numbers 
and so on,
which,
being irrational, were not included in
the fractions already inserted.
The number of such irrationals (and transcendentals), he concluded,
represented a higher order of infinity.
The
Cantor proof has never been convincing to me. Firstly, I am bothered by
the assumption that, because it is possible to set up a procedure for
putting the fractions in one-to-one correspondence with the whole
numbers, therefore the number of fractions is the same as the number
of whole numbers. Again, we have an obligation to distinguish between
numbers that have clear and distinct values (the fractions) and
irrational numbers, which can only be approximated and which, as we will
show, do not occur in nature. There is also the question of whether
infinity is properly a number at all. Is it not by definition that
which lacks the very property numbers denote?
In
any case the Cantor "proof" brushes my feelings aside like
uninvited guests. Since it is these very feelings that I depend upon to
appreciate a mathematical proof and that in fact are the source of
mathematical intuition I cannot in their absence retain my interest in
the subject. This does not dispose me in favor of the proof.
I
am left with a similar feeling when I hear of certain modern
economists who proclaim that it makes no difference how much the
nation goes into debt. But this kind of objection does not refute the
formalism and cannot be used as a valid objection to Cantor's method.
Seeing
the assent of authorities to Cantor's proof, I begin to feel a division
that cuts me off from the pursuit of mathematics, which makes me feel
that there is something misguided about the subject. This sense of
uneasiness often occurs when I study a new subject, and experience has
taught me that this negative reaction to a new teaching generally passes
in a few months.
This
happened when I first encountered some of the facts of aerodynamics,
such as the Magnus effect by which a rotating drum causes the incident
wind to divide and the greater part of it to go around one side. It goes
against common sense that the pressure of air is less on the side
where the greatest amount of air is passing. Ultimately I was able to
satisfy myself that this did make sense, thanks to the realization that
the air at rest presses equally in all directions. When air is forced to
move in one direction the average motion of particles in that direction
increases, which implies that the average motion in the sideways
direction (at right angles to the wind) is slower (the air particles
have a slower motion), creating less pressure or a partial vacuum. This,
the so-called Bernoulli effect, is the reason there is a vacuum on the
upper surface of an airplane wing and is the main cause of its lift.
But
for the fifty-odd years since I first encountered Cantor's proof, I have
discovered no such salutary escape from my first uneasiness.
The
latter part of Cantor's argument, on the other hand, can be more easily
refuted. Having put all the rational numbers in order on a line, so
goes the argument, we
find
that 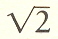 is not represented. We are thus required to conclude that there
are gaps between the densely packed rational numbers, this despite the
fact that there are an infinity of rational numbers between any two that
can be named. Then, the argument continues, since there are an infinity
of gaps, and each gap can be shown to contain as many points as the
original gap (see Figure 12), there must be a larger infinity of points
on the line than have been marked by the rational numbers.
is not represented. We are thus required to conclude that there
are gaps between the densely packed rational numbers, this despite the
fact that there are an infinity of rational numbers between any two that
can be named. Then, the argument continues, since there are an infinity
of gaps, and each gap can be shown to contain as many points as the
original gap (see Figure 12), there must be a larger infinity of points
on the line than have been marked by the rational numbers.
One
could object that since the gaps are infinitely small, it is by no means
clear that they contain an infinity of points. But a more pertinent
objection is that, accepting that each gap contains an infinity of
points, if we stand back and ask ourselves what's going on, we realize
that by putting points in the continuum we are not filling in the
continuum, we are dividing it. We began with one gap to fill; we
now have an infinity of gaps. We must be going in the wrong direction! A
point is discrete. It is a discontinuity. We are reminded that the
continuum is the absence of any point, not a plurality of points. It is
as though we were trying to define an express train by saying that it
makes an infinity of stops, when an express train is defined as one that
makes no stops. So the number of the continuum, if number it is to
have, would be zero.
There
are no points on a line.
Paradise
Lost?
It
is not irrelevant that geometry elects to introduce point and line as
separate undefined terms. Why then should mathematics attempt to define
one in terms of the other, especially as points and lines are not the
business of mathematics? I can only assume that mathematics has gone
astray, or rather that those who attempt to logicize mathematics
have become seduced by formalism. In describing Cantor's proof, even
Courant and Robbins, whose book What Is Mathematics? (1941) is
the best and clearest account of the subject I have found, and who
constantly remind the reader of the importance of intuition and of
practical application, are caught up in the current of the
early-twentieth-century fashion for formalism. More recently, Kline's Mathematics:
The Loss of Certainty (1980) shows that these much-touted
certainties are in deep trouble today. The chapter that especially deals
with this fall from grace is titled "Paradise Barred."
In
Men of Mathematics (1937), Eric Temple Bell also devotes a
chapter, which he called "Paradise Lost," to Cantor and his
proofs. Although I've read this chapter many times I can't make out to
which paradise Bell refers, but he gives a good description of the
controversy, giving a blow-by-blow account of objections to Cantor by
Kronecker ("God made the integers, the rest were made by
man"),
Hilbert and Brouwer. He includes a quotation from Bertrand Russell that
indicates the enthusiasm Cantor inspired:
Zeno
was concerned with three problems. . . the infinitesimal, the
infinite, and continuity. From his day to our own the finest intellects
of each generation in turn attacked these problems, but achieved,
broadly speaking, nothing.
Weierstrass,
Dedekind and Cantor have completely solved them. Their solutions. . .
are so clear as to leave no longer the slightest doubt of difficulty.
This achievement is probably the greatest of which the age can boast.
. . The problem of the infinitesimal was solved by Weierstrass, the
solution to the other two was begun by Dedekind and definitely
accomplished by Cantor. (quoted from R. E. Mortiz, Memorabilia
Mathematica, 1914)
Bell
goes on to say:
The
enthusiasm of this passage warms us even today, although we know that Russell
in the second edition (1924) of his and A. N. Whitehead's Principia Mathematica admitted
that all was not well with the Dedekind "Cut" which is the spinal cord of
analysis. Nor is it well today. . . Not one of the finalities of Russell's
remarks of 1901 survived. . . Today for every competent expert on the
side of the prophets there is an equally competent expert against them. (p. 557)
Rather
than attempt to do justice to the history and changing
status of Cantor's work, let me again introduce what I think to be the
source of the controversy - the failure to realize that a formalism cannot in
principle give a final or complete account. The formalism is a tool
much as a
computer is a tool; it does not answer fundamental questions, nor can it be
expected to. This is because it must be objective, just as language must be
objective, and this precludes it from speaking to the more fundamental
issues, which
are projective. To illustrate the difference, let us examine just one of the
items involved in Cantor's proof, the one that says the number of points in a
part of a line are same as the number in the whole line:
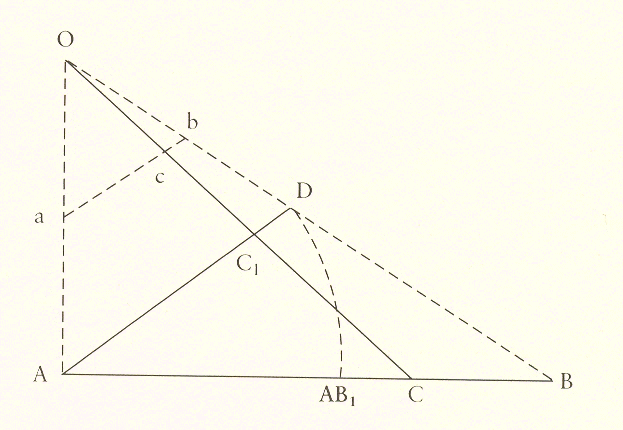
The
line is AB, the part of the line is AB1. Take point
0 not
on line AB. Draw line OB, then swing AB1 to
intersect OB at D. From any point C on line AB we can
project the ray DC, which intersects AD at C1. For any
point C there is a corresponding point C1.
But
note that it makes no difference how far the line AD is from
0.
We could just as well take the much shorter line ab and show that
there is a point c on ab that corresponds to
C. In fact
we could carry the line ab back to 0 where it
Would vanish in
the periphery of the point. But the point is dimensionless, so its
periphery is zero.
In
other words an
infinity of possible directions can be extended from o. (Which recalls
the much-maligned medieval speculation: How many angels [angles] can
dance on the head of a pin? - Infinitely many.) In any case as many
directions extend from the point as there are points in the line. More,
in fact, since for every line OC there is a line in the opposite
direction which does not meet C.
Note
that we are not saying there are an infinity of points on the line; we
are only saying that we can designate as many points by this
method as we have means to distinguish them.
It
is interesting to imagine the practical problem posed by filling
the line with points. Suppose we were to take a line 1 cm long, which is
100,000,000 angstroms. (An angstrom is approximately the diameter of
an atom.) Suppose this line were drawn on the face of a crystal. We
could designate a point at each of the nuclei of 100 million atoms
distributed along the length, but then we would find between each
nucleus a gap 100,000 times the diameter of each nucleus. Aside from the
sheer number of points (now 10 (to the 5th) X 10 (to the 8th) = 10 (to
the 13th), (ten trillion), we would
not be able to deal with these small dimensions because the energy would
go up as we tried to measure smaller dimensions. We would
be prevented from carrying out Cantor's program.
Of
course, you say, Cantor's proof does not purport to be practical, it is
theoretical. This is, however, the main point of the uncertainty
principle. The increased precision cannot in principle be
obtained. The world is bounded by a wall that prevents access to zero
just as effectively as it prevents access to infinity. This limitation
is set by physics, but it depends on first principles; it is not a mere
practical limit, so we are not permitted to ignore it.
The
same applies to Zeno's argument that the arrow at each instant is at
rest and therefore cannot move. The arrow at each instant is not at
rest, because the instant must always have duration, and in this
duration it is moving. So we must ask ourselves how we so easily made
the assumption that the arrow is at rest at each instant when, to put it
bluntly, there is no such thing as an instant.
Is
this "instantaneous view" not a pure presumption manufactured
by mind? A very useful one to be sure, but not to be trusted in an
inquiry into first principles. This view of Zeno's paradox thus disposes
of the idea of higher infinities in much the same way that relativity
disposes of the idea of simultaneity.
Rationals
and Irrationals
The
Cantor proof of higher infinities depends upon the notion that there is
an uncountable number of irrational numbers that can be located in the
continuum as points on a line. In "The Queen and Mr. Russell,"
I made the point that there is a fundamental distinction between putting
rational fractions on a line and putting the irrational numbers on a
line, in that the geometrical construction that produces an irrational
on the plane (e.g., 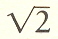
as the
diagonal
of the unit square) has to be transferred to the line. As I said
in that essay, the square root of two is an inhabitant of the plane,
not of the line.
I
now suspect that this doesn't get to the heart of the problem, which
involves the distinction between a linear dimension and the two
simultaneous dimensions of a plane. The fact that we can draw a line on
the plane is misleading, because the line on a plane permits comparison and measurement. If we were confined to one
dimension we
could not measure, because the ruler and that which it measures could
not be separated. (See "A Formalism for Philosophy" and
"Constraint and Freedom" in Which
Way Out [1980].)
Perhaps
the simplest example of dividing the line involves the string of a
musical instrument, which would normally vibrate at the lowest
frequency, the "fundamental."
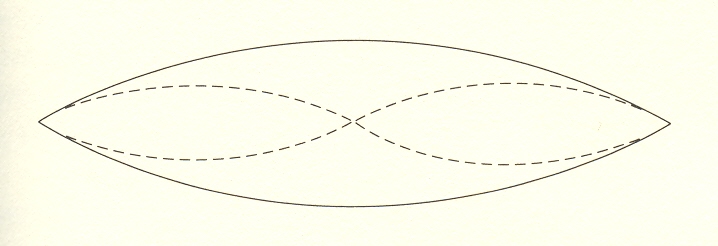
When
the string is restrained at its center, it will vibrate at twice the
fundamental; when restrained one-third of the way, at three times the
fundamental, and so on. This provides a way of creating fractional time
intervals. It does not depend on the exact distance; it is in
the nature of the string to vibrate at these integral values of
frequency. The same thing occurs in quantum phenomena - the frequencies
of atoms are in an integral relation to one another (eigenstates).
Another
example of rational or exact fractional division of time can be
produced with gear wheels. Two shafts can be caused to rotate at speeds
with an exact ratio by making gear wheels the number of whose
teeth are in the required ratio. This does not depend on the accuracy of
the gear teeth, just on their number. An irrational ratio cannot be so
produced.
This
implies that there is a sense in which the irrational numbers are
abstractions that are only encountered through measurement or
calculation - they are "components" of the natural numbers.
They do not themselves occur in nature. Thus, instead of considering the
diagonal of the unit square as 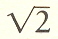 ,
we could consider that the sides of a
square whose diagonal is 2 are
,
we could consider that the sides of a
square whose diagonal is 2 are 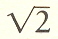 .
.
This
is well illustrated by the device of describing the circle as the locus
of points from which two rays at right angles meet the ends of a line
that is the diameter of the circle:
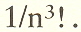
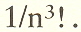
We
can think of the line AB as the unit and the lines AC
and CB
as "components." We only encounter irrational numbers in
nature when we compute the value of such components.
The
Ideal and the Real
By
engaging our minds in proofs and demonstrations that are often quite
elegant, mathematics leads us to believe that it deals in an ideal
world, one removed from the jumbled confusion of phenomena, a world
that is unchanging and perfect. This view of mathematics as "the
world of pure form," of "certainty of results,"
exemplified in the proofs of geometry and in almost all purely
mathematical operations, seems to contrast sharply with the approximate nature of human and natural
constructions - the variety and
deviation from the ideal that characterizes the world of physical
objects.
But
the findings of science in the last hundred years point toward an
opposite conclusion. The works of nature are, in fact, extremely
precise, perhaps perfectly precise.
Nowhere
is this precision more in evidence than in the atomic kingdom. The
simplest demonstration is the fact that all atoms have been found to be
organizations of an integral number of proton/electron pairs,
which give what is known as the atomic number.
A
further example of the extreme precision of the atomic world is
illustrated in the Mossbauer effect, by which it is possible to measure
a motion of a few centimeters a second by the variation in absorption
of radiation by the nucleus of the atom. This process implies an
accuracy
of
frequency response better than one part in ten billion, far beyond our
ability to measure. The nucleus of the atom exercises this
discrimination despite the fact that the wavelength of the incident
radiation is about six thousand times greater than the diameter of the
nucleus.
Again
we have atomic clocks, which have replaced the rotation of the earth as
a criterion for measuring time. The
atomic
clock can measure a variation in the earth's rotation of less than one
second per century. This exact precision is far beyond our ability to
measure in any other way and hence establishes a standard that may well
be absolute.
But
such precision is not confined exclusively to the atomic world. The
immune system of the human body has the capacity to detect the presence
of an organ transplanted from anyone of some four billion other
inhabitants of the globe, a discriminatory power on a par with that of
atoms.
What
all this suggests is that "the world of pure form" is not
confined to the celestial sphere. Nor is it to be found only in pure
mathematics. The material world, in its own way, is incredibly, perhaps
infinitely, precise.
The
Dedekind Cut
This
question of "real" perfection can help clear up the difficulty
surrounding one of the well known "proofs" of mathematics, the
so-called Dedekind cut. The Dedekind cut involves the same problem as
Cantor's proof of higher infinities, since it proposes a system for
locating irrational numbers in the continuum. It has, however, long been
questioned for its own implicit treatment of infinity.
Dedekind
was troubled by the problem of putting 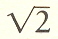 on the line between one and
two. His method was to assume a rule that divides all natural numbers
into two classes, in this case the class of rational numbers less than
on the line between one and
two. His method was to assume a rule that divides all natural numbers
into two classes, in this case the class of rational numbers less than 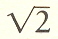 and the class of rational numbers greater than
and the class of rational numbers greater than 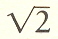 .
. 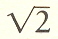 is thus the
"cut" or gap between these classes. (It is assumed by
some mathematicians that the Dedekind cut can be achieved without
reference to geometry, but doing so
would still involve a quadratic equation, and hence two orthogonal
dimensions.)
is thus the
"cut" or gap between these classes. (It is assumed by
some mathematicians that the Dedekind cut can be achieved without
reference to geometry, but doing so
would still involve a quadratic equation, and hence two orthogonal
dimensions.)
Dedekind's
method depends, as did Cantor's system, on infinitely small distances or
measures. And since, as we have seen, the infinitely small, whether in
distance or time, is only obtainable with infinite energy, it is
impossible to achieve.
The
standard objection to such an argument is that in mathematics we are not
concerned with practicality; we are dealing in theory. (Eddington once
said he would never have proposed 10 (to the 79th) as the number of protons in the
universe if he thought anyone was going to count them.) But here we
have the case of practice and theory merging in the Heisenberg
uncertainty principle.
The
uncertainty principle is a consequence of Planck's discovery that action
comes in whole units that cannot be less than a certain size, a sort of
indivisible "atom" of action. So deeply does it penetrate
into the foundations of physics that the distinction between theory and
practice breaks down. A similar import could be claimed for the speed of
light and a small number of other constants of nature. These constants
are at once empirical and theoretical, empirical because their values
are found by experiment, and theoretical because, once found, they
become the basis for theoretical deductions.
The
question then becomes, does the theoretical limit to smallness that
physics has been obliged to accept (to its ultimate benefit) penetrate
into mathematical theory? The ready answer, again, would be no. But
insofar as mathematics deals with first causes it can no longer indulge
this separation of fact from theory. We can formulate this as a
principle: An operation
that cannot in practice be performed should require that the theory be
revised to anticipate
the practical limitation.
We
will come back to this issue later.
The
Transcendentals
Is
it possible that Cantor had a valid insight but, as is often the case,
distorted it by misinterpretation? Essentially what he says is that
there is something beyond infinity.
Perhaps
by introducing some ideas I've had for a long time together with the
conclusions we've reached here we can arrive at a speculation that would
account for Cantor's inspiration and justify some of the acceptance he
has been accorded. However, these ideas, while reasonable and
straightforward, are even more foreign to what is accepted in
mathematics than were Cantor's - in fact, we could say that Cantor's error
was to accommodate to the usual thinking.
The
ideas to be put together are:
1.
Numbers can better be defined as successive divisions of unity
rather than as additions to unity as Peano's axioms assume. (This is a
point developed in "The Queen and Mr. Russell." I have
recently noticed that Eddington says the same thing in The
Philosophy of Physical Science: "Wave mechanics thus brings
the integers [which form the whole material of our ordinary
arithmetic] into its purview as the eigenvalues of one of its symbolic
operators. Introduced in this way the integers are concepts
unassociated with the procedure of counting." [p. 173])
2.
There is but one transcendental number,  or two if you count e as
independent of
or two if you count e as
independent of  . (e is related to
. (e is related to
 by the formula:
by the formula: 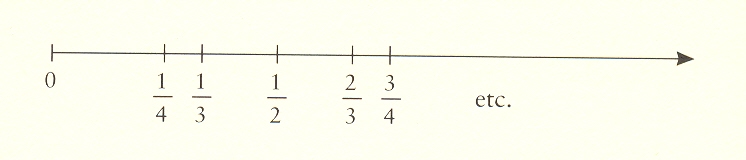 =-1. I should acknowledge the fact
that
there are large classes of numbers that have been proved to be
transcendental in the sense that they cannot be expressed as roots of
equations, such as
=-1. I should acknowledge the fact
that
there are large classes of numbers that have been proved to be
transcendental in the sense that they cannot be expressed as roots of
equations, such as  +
+ 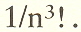 . Others, such as
. Others, such as
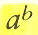 where b
is irrational, are neither constructable nor do they possess the
same empirical status as
where b
is irrational, are neither constructable nor do they possess the
same empirical status as  or e.
or e.
It can be argued that
neither of the above classes of number "exists" apart from
their definition. A theoretical number such as a transcendental, I
would argue, must have some foundation in nature. In fact, if the
prescription for a number were sufficient to affirm its existence, one
should include unicorns, griffons, manticores, and other fabulous
animals in zoological classification, of which animals found in nature
would be a subset.)
3.
The line or continuum does not consist of an infinity of points, nor
of more points than can be put in correspondence with the infinity of
natural numbers;
rather
the point itself makes possible the projection of an infinity of directions.
Proceeding
from these assumptions, we will find that the construction that would
establish directions depends on our ability to divide the 360°
circle - of
which 
is the signature - implied by the point. (The point is a
circle of arbitrarily small radius.) Such construction would limit us to
rational divisions of the circle.
The
circle represents wholeness. In the process of dividing we would
discover that each number (or perhaps each prime number) provided a
unique division not obtainable by other divisions. For example
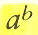
-
an
infinite series of smaller and smaller terms.
Note
that if we replace one of the 1/4's, for however small a term (i.e.,
however high a power of the denominator), by 1/3, the infinite series
collapses into an identity. Thus:
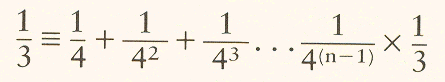
To
define  in terms of an infinite series we use Euler's formula:
in terms of an infinite series we use Euler's formula:
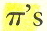
In
other words,  is unique. Unlike the integers, which are expressible in
terms of one other number,
is unique. Unlike the integers, which are expressible in
terms of one other number,
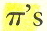 expression requires all the
numbers (or all
the odd numbers).
expression requires all the
numbers (or all
the odd numbers).
Other
examples share this propersity:

can
also be expressed as an infinite nesting of square roots.
Passing
beyond technical considerations, such as whether these are the best or
most general expressions of the principle, to an interpretation of
the principle, we could say 
incorporates (or implies) all the natural
numbers. And since each number can be expressed as an infinite series of
inverse powers of the next higher number,  can be
represented as an
infinite series of infinite series.
can be
represented as an
infinite series of infinite series.
However,
 is not quantitatively infinite. In Euler's expression (given above)
addition and subtraction alternate, and the sum approaches a certain
value between 2/3 and unity. So
is not quantitatively infinite. In Euler's expression (given above)
addition and subtraction alternate, and the sum approaches a certain
value between 2/3 and unity. So  is quantitatively finite, but
includes an infinity of qualifications (natural numbers), each of which
is itself "infinite"
in the sense that an infinite series is required to express one number
in terms of another.
is quantitatively finite, but
includes an infinity of qualifications (natural numbers), each of which
is itself "infinite"
in the sense that an infinite series is required to express one number
in terms of another.
We
thus associate  with an infinity of infinities, and since
with an infinity of infinities, and since  is
transcendental, we could say that Cantor correctly perceived that
transcendental numbers are" beyond infinity." But two
misinterpretations confused Cantor's fundamental insight: 1) that
infinity is a very large quantity; and 2) that what is beyond
infinity is a still larger quantity - i.e., that there are an
uncountably infinite number of transcendental numbers.
is
transcendental, we could say that Cantor correctly perceived that
transcendental numbers are" beyond infinity." But two
misinterpretations confused Cantor's fundamental insight: 1) that
infinity is a very large quantity; and 2) that what is beyond
infinity is a still larger quantity - i.e., that there are an
uncountably infinite number of transcendental numbers.
To
put this in perspective, it could be said we have inverted Cantor
and even Peano. Peano defined number as successive additions to one.
This fails to bring out that a number is not just a collection of n units,
it is a unity of n parts;
that is, any number, say five, is both a collection of five units and a
unit of five parts. Once this is recognized, the definition of number as
successive divisions can be appreciated.
The
inversion of Cantor is justified because there does not, in fact, appear
to be an infinity of transcendental numbers. Among numbers having any
application to the real world, 
and e alone have been proved to
be transcendental. These two numbers are intimately related, and it is
possible that they are not "different" numbers but aspects of
the same "non-number." Since we define numbers as divisions of
the whole, and  is not a division but the whole itself, it is not a
number.
is not a division but the whole itself, it is not a
number.
Thus,
while preserving Cantor's distinction between
transcendental
and other numbers, we view  as the transcendental
number. It is preeminent not because it is one of a higher infinity, but
because it is unique.
as the transcendental
number. It is preeminent not because it is one of a higher infinity, but
because it is unique.
We
may in fact think of  as a super number, the
as a super number, the
source
of all of the other numbers. We can say this because  represents the circle, a symbol for wholeness. The integers can be
defined as the angular division of the circle. This also provides a
definition for fractions, since given the concept of division - that the
whole can be divided into n parts - each one of these is 1/nth of
the whole. The real numbers can be accommodated or defined as
trigonometric functions, i.e.,
represents the circle, a symbol for wholeness. The integers can be
defined as the angular division of the circle. This also provides a
definition for fractions, since given the concept of division - that the
whole can be divided into n parts - each one of these is 1/nth of
the whole. The real numbers can be accommodated or defined as
trigonometric functions, i.e., 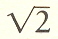 is twice the sine of 45°, and so
on. (This might comfort the ghost of Pythagoras.) I do not know whether
all algebraic numbers could be expressed as trigonometric functions,
but a plane surface does accommodate solutions to equations.
is twice the sine of 45°, and so
on. (This might comfort the ghost of Pythagoras.) I do not know whether
all algebraic numbers could be expressed as trigonometric functions,
but a plane surface does accommodate solutions to equations.
Whether
or not this approach to number is more correct than the one now in
use, it is safe to say that the current
interpretation of natural numbers as a mere subset of larger classes of
numbers is not a useful one. If the question is one of elegance or
aesthetics, which are valid criteria in mathematics especially, then I
regard the descent of all numbers from the unity of 
as the more
elegant description.
Philosophically,
too, it is better to think of the universe as unity with infinite
diversity than as an infinite collection, countable or uncountable. This
notion, as we've pointed out, allows for quality as well as quantity. I
suspect this issue is involved in Bohr's complementarity principle,
which is generally interpreted to mean that for one measure to be made
precisely, another measure must be imprecise. We would extend this to
read that any measurement must be complemented by a quality that is different
from measure. Measurement of size, for example, is incomplete
without a reference to an actual object to provide scale.
In
other words, quantitative measurement is in principle incomplete.
Applied to mathematics, this implies that if mathematics is the
science of quantity, it cannot deal with
first
principles; or alternatively, if mathematics is to deal with first
principles - if it is to be queen of the sciences - it must recognize that
which is not quantitative, which we here call quality.
The
transcendental number  is one way in which the limitation of
quantity shows up.
is one way in which the limitation of
quantity shows up.  is neither large nor small, but it cannot
be expressed in finite terms.
is neither large nor small, but it cannot
be expressed in finite terms.
Cantor's
mistake was to find preeminence in the quantity of
transcendental numbers, whereas it is the quality of the
transcendental itself that makes it unique, that makes it the
"origin" capable of any direction. There is a oneness beyond
everything that cannot be described because it is beyond everything.
This oneness includes all that
can
be described.
Mathematics,
Physics & Reality
Mindfire

is not represented. We are thus required to conclude that there are gaps between the densely packed rational numbers, this despite the fact that there are an infinity of rational numbers between any two that can be named. Then, the argument continues, since there are an infinity of gaps, and each gap can be shown to contain as many points as the original gap (see Figure 12), there must be a larger infinity of points on the line than have been marked by the rational numbers.