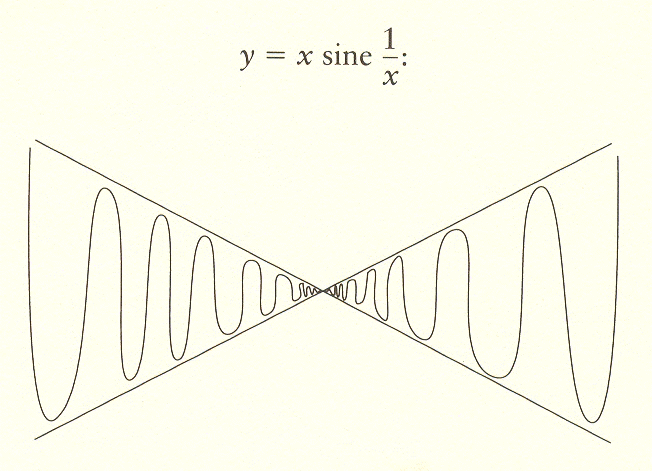*
RIGOR MORTIS
In What is Mathematics? Courant and Robbins comment on the swing from intuitive mathematics in the seventeenth and eighteenth centuries to the emphasis on formalism in the nineteenth and twentieth. The emphasis on formalism is credited with contributing increased rigor to what were formerly intuitive insights.
Systematic deduction disappeared in the 17th and 18th centuries. Logically precise reasoning starting from clear definitions and non-contradictory "evident axioms" seemed immaterial to the new pioneers of mathematical science. In a veritable orgy of intuitive guesswork... they conquered a mathematical world of immense riches. Gradually the ecstasy of progress gave way to a spirit of critical self control. . . the 19th century not only became a period of new advances but was characterized by a successful return to the classical ideal of precision and rigorous proof. (p. xvi)
As an example of this new rigor in mathematics, in 1925, when I was in college, there was great emphasis placed on the Cauchy proof of the existence of a derivative of a function at a point. This made calculus difficult, for it made what seemed obvious, that a line had a slope at a point, become dubious and hard to understand; moreover, it struck me at the time that it was not a "proof." The Cauchy technique depends on your first selecting a very
small number 1:; then I show that I can find a value 6y (6 means a small increment) in the ratio 6y/6x such that 6y is less than 1:; then the derivative 6y/6x can be said to approach a definite limit dy/dx, which is the derivative.This was not convincing, because it permitted me to have the last word. It was as if I could prove the validity of a signature by requiring you to name the permissible deviation from a genuine signature; then I would only have to produce a signature that deviated less than the permitted amount, and you would be obliged to accept it as valid.
In any case it distracted from the main issue, which was to see the great power of the calculus and use it. It was not until years later, when I could use calculus in practical problems, that I felt comfortable with the subject.
The assumption that the derivative at a point can be reached by successive approximations, as with the Cauchy proof, applies only for so-called analytic functions. This limitation would exclude certain curves - for example, a curve with a break at a point S:
This curve has no definite tangent at this point and hence
no derivative. Another more complex example is the function
When I read such accounts in the past I usually thought of them as exceptions, and rather artificial ones at that, which could be ignored. But now I realize that there are situations that are not artificial but that at the same time do not profit from this sort of mathematical treatment. In fact, some interesting positive consequences arise if we free ourselves from this misguided obligation to provide mathematical rigor and heed instead the obligation to respect the workings of nature.
Consider this curve, representing a person driving a car and turning a corner:
Such a curve has a derivative. (Each of the following curves portrays the rate of change of the previous curve):
The direction of the car changes, say, from due west to northwest. What is the second derivative?
The curve
The 1st derivative
The 2nd derivative
The 3rd derivative
The 4th derivative
and so on. The derivatives become increasingly complex and serve no useful purpose since the analysis of the rate of change does not simplify our treatment of the motion.
What gives the first curve its "non-analytic" quality is that the driver has decided to turn. Decision is not predictable. And if this seems unfair, there are situations or phenomena in nature that yield the same result.
One example would be a tsunami (a so-called tidal wave). Ordinary tides can be analyzed into a number of cyclic components, and if we find what these components are by study of tides in the past, we can make a prediction of their behavior in the future. Not so with a tsunami. If caused by an underwater volcanic eruption or an earthquake, it cannot be predicted by study of tides in the past. It comes without warning and is not predictable - not subject to analysis - and is furthermore useless for predicting future tides or tsunamis.
Let us see what this means. Analysis for the most part consists in a recognition of the factors that contribute to a situation on the assumption that these factors have always been in operation. In the case of tides these factors are cyclic - the position of the moon, the position of the sun, and such other variables that continue through time. These variables change, but their change is periodic and can be predicted. This could be called a conservation law; the factors involved do not arise spontaneously and do not vanish spontaneously. Energy is neither created nor destroyed.
On the other hand there are, as I said, phenomena that cannot be predicted by the analysis of cyclic components, e.g., volcanic eruptions and earthquakes. This latter class of events has been ignored by theoretical science for much the same reason that discontinuous functions have been ignored by mathematics - they do not lend themselves to mathematical treatment. (Recent efforts to predict earthquakes by careful study of the earth disturbance immediately prior are not an exception. Such study is advanced warning rather than analysis. Even if predicted, the eruption is a unique phenomenon, with a beginning and ending in time.)
But uneasy lies the head that wears the crown. The provision of absolute rigor within mathematics, admired by Courant, does not address the more awkward question of applicability. The fascination with rigor has in fact resulted in the assumption that all nature must be subject to analysis by rigorous approach. Again in physics, the insistence on objectivity of method has led to the dogma that
nature is exclusively object.But nature hasn't studied continuous functions and goes ahead with its discontinuities - not only earthquakes, but people making decisions. Any decision has a component of initiative, and hence of what has no antecedent.
Hierarchy and Control
It becomes useful, then, to distinguish aspects of nature that can be analyzed from those that cannot. The formalism can deal with the former, often with impressive results, but we must not become so attached to formalism as to regard it as a first principle. Formalism is a means. Whatever it is that can employ formalism to produce results that are seemingly at odds with the laws described by the formalism - such as when a bird or a flying machine "defies" the law of gravity - has a more basic status than the formalism itself. Purpose, or intention, can be so designated and thus qualifies as first cause, as distinct from formalism, which is secondary.
Our problem is to set up a formal system that admits first cause; call it a super-formalism. This is where science, by its exclusion of purpose from its methodology, and mathematics, by its self-limitation to formalism, both disqualify themselves from the discussion. Even philosophers have to remain silent on this ultimate question, for any attempt to describe the ineffable involves a self-contradiction. As Wittgenstein said, "Whereof one cannot speak one must remain silent."
Nature, however, offers a clue that enables us to get to the root of the problem rather than remain entangled in the limitations of language.
Many phenomena in nature involve these cycles within cycles. The animal organism is subject to a hierarchy of cycles: waking and sleeping, breathing, heartbeat, brain waves, on down to the range of frequencies involved in cellular and biochemical processes, which themselves cover a vast spectrum, from extra-long (ELF) waves to the infrared frequencies of photons exchanged in cell division. Since the organism begins from division of a single cell and grows to an organization of trillions of cells, the process of building the organism must require the simultaneous erection of a chain of command by which the entire hierarchy is controlled. Even if we do not accept the validity of such super-normal abilities as fire walking, or disregard such well-established phenomena as the ability under hypnosis to produce burns, we still have the problem of how we can lift even one finger or produce any voluntary action. Voluntary action and even action controlled by instinct require an elaborate hierarchy.
One salient point emerges. Considering the whole range of frequencies involved, from that of the alpha rhythm (10 per second) to that involved in metabolism (trillions per second), we can reasonably surmise that the lower frequencies characterize the larger "organon." (A term I employ to indicate any self-organizing entity, not necessarily biological.)
It is also obvious that the larger organon could not have evolved from a single cell without being able to control and coordinate the activities of its constituent parts. This implies that the lower frequency controls the higher frequencies. This is difficult to accept, because the higher frequencies involve greater energy exchange. However, all man-made machinery involves control of energy, and if the energy controlled were not greater than the energy needed to control the machine, machinery would be useless.
This is consistent with the relationship between energy and time decreed by Planck's Constant, in which energy is inversely proportional to time (e x t = h); that is, if we reduce the energy, the period increases. The significance of this is that the organon which spans the longer time controls processes that span the shorter time. Put in terms of human actions, you can only control a process shorter than your attention span.
But how does control function? Process goes through a cycle, and control selects the phase or stage in the process it desires. The gardener picks the fruit when it ripens rather than letting it go to seed; the photographer snaps the picture when the sitter smiles, etc. This is correct timing.
Modulo and Residue
I will now introduce the notion of modulo and residue. This idea describes, for example, the process of counting
in the decimal system. Such counting consists of running through the numbers zero to nine, then continuing with one followed by each of these digits, then two followed by each digit and so on. The term modulo is applied to the number of units of 10, and the term residue to that which remains after division by 10. Thirteen, then, is modulo 1, residue 3. Twenty-seven is modulo 2, residue 7. And so on.We thus distinguish the number of completed cycles as modulo and the final incomplete cycle as residue.
We reckon time in this way when we give the date; say, the 26th of February, 1985. 1985 is the modulo or number of completed years; February, the second month, implies the completion of January and 26th the completion of 25 days. Still further precision would be supplied by specifying the hour, minute and second.
Whether we simply name the current date or describe history, the distinction between what has occurred and what is still in process is fundamental. We can only conceptualize or name that which has already taken place. We cannot so deal with the future or the present until after the cycle of which it is a part is completed.
Thus, as I write and form the letters of the word "word," I am continually incorporating the present into the past; what is now present tense becomes past tense. I act only in the present. I can also think in the present, but the object of thought is not in the present, the now, and my
present activity is never the object of thought. This distinction is intrinsic in language. Applied to sentence formation, the verb in the present tense is the residue, and the object of the sentence is the modulo.In general, the distinction between modulo and residue is the same one we made earlier in our discussion of quantity and quality.
So far, however, the distinction we have drawn (between modulo and residue) is based only on whether or not a cycle has been completed. What we should now recognize is that as the process of repeated cycles continues, we become conscious of larger cycles. Thus in counting we first can be aware of units of 10, then of units of 100, then of 1,000 and so on. In life our awareness is enriched by the perception of long-term trends or variation; if we have lived through the changes of the twentieth century, the fashions and tastes we have witnessed lose the hold they once had on us. We become more able to think independently, to distinguish lasting from transitory values, and thus to set long-term goals.
This in turn affords a clue as to how the hierarchy of a living organism comes about. The long period cycle of consciousness comes into existence because of the passage of time. This could be a valid instance of emergence, a notion that is often evoked to "explain" consciousness. While we would still insist that the concept of emergence is not sufficient to account for consciousness, the view expressed here does explain how consciousness can expand to take into consideration "larger" issues - actually issues of longer duration - and thus increase its scope from that of a bacterium to that of a higher animal. This, in fact, could be a critical difference between the human and the animal consciousness. The average human life span is more than four times that of the higher animals. This longer period, which has no genetic advantage for man as a species (since the genes are not influenced by acquired experience), does influence the evolution of individual persons.
It is generally assumed that science cannot deal with such questions as the evolution of consciousness. But if we attend to the history of science, we find the development of science hangs on two things. First, the discovery or invention of tools such as the telescope, the microscope and the spectroscope, which extend the senses and expand the database of empirical fact. And second, the discovery or invention of mathematical tools like the number system, probability theory and the calculus, which extend the power of theoretical analysis.
The development of the computer has already spawned a new school of philosophy, which, recognizing the difference between the hardware and the software of the computer as analogous to the difference between the brain and its function, seeks to account for the mind-body problem. This can be a valuable contribution, but it can also increase the already serious imbalance that has accompanied technical progress. In fact, the computer, the functions of which duplicate formal logic, is a device limited by just the mathematical formalism I am criticizing in this essay.
What we need, then, is a formalism that gives legal status to life, or perhaps rather to the innovating and creative aspect of life, its purposive thrust, since it is this aspect that is neglected in the computer analogy because it resides in the person using or programming the computer. The notion of residue as used here addresses this issue by providing for an ongoing creative activity in the present moment.
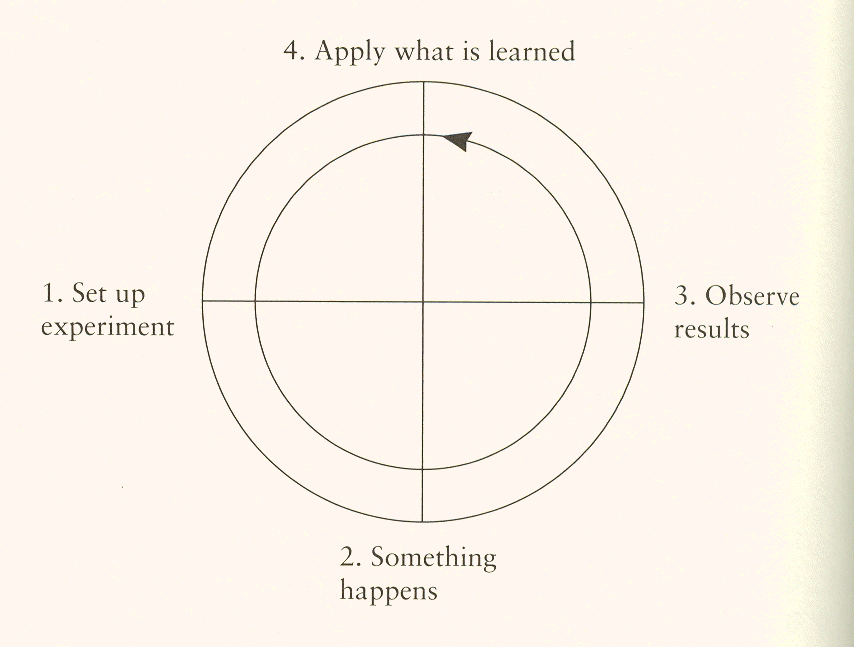
We have already stressed the importance of the third derivative as that which allows for control, and hence makes it possible for will to use the laws of nature to effect results. But the recognition of control is not enough. The vital principle, or life spark, that evolves by use of control must also be acknowledged. Quantum physics goes part way to this acknowledgement by recognizing the role of the observer. What it fails to acknowledge is that the observer also acts; in fact, in any cycle of action, acts twice, the first action being inquisitive and the last being with knowledge of consequences. The "observation," which the physicist acknowledges, takes place in between these acts. Applied to the physicist, the cycle of action then reads:
Such a cycle occurs in the plane of qualification, i.e., it has four phases which are categorically different. The repetition of this learning cycle accumulates as memory or modulo. The last cycle, which is always incomplete and always growing, is the residue. This is the one in the present tense; it is also the one that cannot be made the object of consciousness and can never be certain, cannot be explained, does not in fact exist, though it always is.
Mathematics and Meaning
In the last year of my college life my younger brother died. The event produced a profound impact on me. It called my attention to the fact that time brought surprises and that formal theories of cosmology, such as relativity, which treated time as a dimension like space, and hence as essentially predictable, failed in an important respect.
The so-called Cretan Paradox, which Russell had written about (so and so says that all Cretans are liars, but so and so is a Cretan), impressed me as being a paradox only because the importance of time was neglected in logic. The statement implies a judgment "that everything so and so has said is a lie." It cannot apply to the statement itself because the statement hasn't yet been completed. (The statement itself is residue, not modulo.)
This recognition of the importance of time, and of the fact that logic and other formal structures cannot encompass the change or flow of time, led me to change the theory of cosmology I wanted to construct from a theory of structure, which is what I first called it, to a theory of
process, which is the theme of The Reflexive Universe.My emphasis in the present work is not just the importance of time, but the importance in mathematics of meaning. I have already done what I can in The Reflexive Universe to correct the error of the neglect of time implied by the emphasis on relationship structure and "objectivity." I now want to stress interpretation and meaning. Here I am not content to have meaning, or if you like philosophy, put in a department by itself, with mathematicians (and by their example other scientists as well) disclaiming responsibility for meaning by saying that they "don't know what they are talking about nor whether what
they are saying is true." No, I believe this attitude has outworn its usefulness; it is time for a change. Such a change, which I trust will not be a reform of mathematics but a challenge to greater achievement, is indicated not merely because philosophy and religion as the search for truth have deteriorated until they no longer inspire and sustain us, but because mathematics itself has lost its vitality.The formalism Courant was still able to extol in 1939, despite shortcomings that had turned up, is now in greater straits. As I've mentioned, Morris Kline documents the current status of the subject in detail in Mathematics: The Loss of Certainty. Kline shows that most of the much touted "rigor" has not held up; as his title suggests, uncertainty has risen from its ashes.
I am of two opinions about this loss of certainty, both of which view it as beneficial - the one because it might well put an end to the pious nonsense of logical positivism that has been in vogue for the last fifty years or so (or a hundred if we go back to Cantor), and the other because the factor of uncertainty is not undesirable. Uncertainty is
what makes life alive. It may be difficult to deal with, but if there were no basic uncertainty, there would be no life and no freedom. As I have shown at length in The Reflexive Universe, the quantum of action, i.e., uncertainty, is responsible for the initiation of life and evolution. To understand this positive contribution of uncertainty we need to go back to our discussion of the derivatives.The third derivative bears the label "With this key you can make determinism serve free will." Physics on the other hand is interpreted to imply that all macro objects obey strict laws of determinism and there can be no free will.
Why is physics so interpreted? Because, as I said earlier, physicists cite the theorem in mathematics that states if you know a function and all its derivatives at one point you can predict it for all other points. But is this a correct interpretation of the derivatives? Most physicists would say yes. Most mathematicians would not comment. But since the third derivative is control, which makes prediction theoretically impossible, and since derivation is a mathematical concept, I believe it is the business of mathematics to put correct labels on the products it turns out. It cannot retain its authority as queen of the sciences if it declines to say what its formulations mean. Someone has to interpret the third derivative. Engineers who work with control systems know; but engineering is not high on the totem pole. If it is the job of physicists to interpret the third derivative, then why do Bohm and de Beauregard, who are good physicists, not recognize the implication?
It's clear that there is a problem. How has it come about? Note that what makes the problem difficult is that it results directly from the division of science into separate disciplines. It even goes back to the division between church and state, between the world of spirit (in which I list free will) and the world of matter, the study of which is the business of science.
In the past four hundred years we have seen the prodigious growth of science and its increased prestige, so much so that the well-informed or well-educated person today
takes science rather than religion as the touchstone of truth. If he does retain some misgivings about science he certainly would not challenge Bohm's assertion that there are scientific formulae that can predict the shape of curves. It would not occur to him that the act of driving a car invalidated the premise of determinism.In short, we have the public, and the educated public especially, not only accepting the findings of science but believing its dogma. The protests of a few philosophers and writers against letting science bulldoze our human aspirations into highways and airports are as futile as beating on the bulldozer with bare fists.
But what if there were within science, embedded in the same formalism that is advertised as determinism, the very thing that inverts that determinism? Is it not incumbent on science to let it be known? If control is part of the formalism, why is it not recognized? Tell it to the judge, says the scientist, reverting to his role as policeman enforcing the laws. Who is the judge? I think we have to turn to mathematics.
But I am arguing the case in too negative a manner. Let me stress the positive side of what I am calling the significance of mathematics, or, if you like, of physics.
Understand that I am not, as was Jacob Bronowski, arguing for the creativity, the poetry, the beauty that the scientist experiences when engaged in scientific discovery. I am talking about the interpretation of science by its practitioners, who insist that science consists only of statements of relationship - of an abstract formalism that maps reality and has no reference to value and to creativity, to emotion and free will.
What is significant is that the most important findings of science do not have to do only with statements of relationship. Science has discovered the non-objective to be even more fundamental than the objective, uncertainty to be more fundamental than certainty. It has, in short, discovered that what it formerly insisted had no relevance to science is fundamental. In other words it has discovered the intangible and non-objective equivalent of spirit at the heart of matter.
The Reflexive Universe tells this story in terms of physics - the quantum of uncertainty, the equivalence of the learning cycle to the cycle of action, the primacy of forces and their priority to matter, the fact that fundamental particles have no identity, the negentropy of living creatures, etc. It is a reinterpretation of physics, chemistry and biology to provide a unified theory of process in which life, far from being "a green scum on a minor planet," is the main purport of cosmology. Such, then, is my brief. I have presented the case at the court of physics and have received little reply. Such few physicists as have commented have told me that what I have to say is not physics, it is philosophy.In the present work I take the case to a higher court, that of mathematics, but not because the subject is more fitted to mathematics. It is probably even further removed from the actual practice of mathematics than it is from the practice of physics. I appeal to mathematics rather because the question of first principles is my most basic interest. It was this interest that led me to major in mathematics when I went to college. Physics fascinated me; it always has. But despite my interest in making things, it has been the light of abstraction shining through practical experiment that has most deeply motivated me.
I would prefer not to drag in the notion of God at this juncture, not only because the age has turned away from the outworn dogma of most religion, but because any mention of the ineffable is self defeating; what is sacred cannot be talked about. I do know there is something beyond myself, something higher than anyone or anything I've known. I know this not only because the best efforts I can contrive point toward it, but because something far beyond me has guided me. I make this statement not as a
claim on behalf of my fallible efforts, but because it is the blood and life that prods me to seek.But this is not physics, I'm told. Then what has inspired physicists? And if it is not mathematics, then what have mathematicians attuned themselves to? And if it is neither, who is minding the store?
I'm sure that many people, today especially, seek this light. They will tell me it is not to be found in science. But, I ask, why not? Can it be found in today's art? In writing? I will tell you where I see it. I see it in what science and mathematics hide from themselves - not the order that science seems so insistent is there - the order that it claims governs chance, the precision with which it calculates what happened nanoseconds after the Big Bang - but in the fact of life and its spontaneous origin, its self-maintenance, its self-transcendence. I see it in people, each one of whom is different from all others, no two of whom will agree, even though truth is one. I see it in time, which produces the unexpected. I see it in what is beyond my comprehension, not because it is incomprehensible but because its very incomprehensibility promises comprehension. I court mystery so that I will have more mystery. I would solve problems to prepare myself for greater problems. In short, I evolve; and because I am evolving, I am.
Mathematics. Physics & Reality